هندسه یازدهم فصل اول

هندسه یازدهم فصل اول موضوع اصلی این مقاله است، در ابتدا به سراغ تعاریف و مفاهیم اولیه خواهیم رفت.

دایره: فرض کنیم O نقطه ثابت و r شعاع حقیقی مثبت باشد. دایره به مرکز O و شعاع r، مجموعه نقطه هایی از صفحه است که فاصله ی آن ها از نقطه O برابر r باشد.

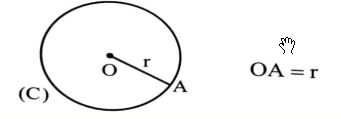
توجه: دایره C به مرکز O و شعاع r را به صورت C(O,r) نمایش می دهیم.

نکته: دو دایره با شعاع های مساوی با هم برابرند.

اوضاع نسبی نقطه و دایره

• اگر نقطه A درون دایره C(O,r) باشد، فاصله ی آن تا مرکز دایره، کم تر از شعاع دایره است.

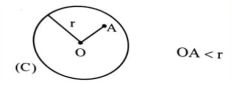
• اگر نقطه A روی دایره C(O,r) باشد، فاصله آن تا مرکز دایره برابر شعاع دایره است.

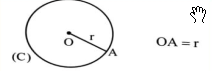
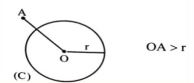
• اگر نقطه A بیرون دایره C(O,r) باشد، فاصله آن تا مرکز دایره بیشتر از شعاع دایره است.

خط مماس بر دایره و خط متقاطع با دایره در هندسه یازدهم فصل اول

خط مماس یکی از موضوعات اصلی هندسه یازدهم فصل اول میباشد که باید به آن توجه ویژه ای داشت.

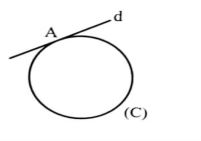
خط مماس بر دایره: اگر خط و دایره فقط در یک نقطه مشترک باشند، می گوییم خط بر دایره مماس است.

در شکل مقابل خط d در نقطه A بر دایره (C) مماس است.

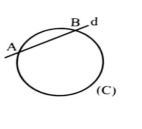
خط متقاطع با دایره: اگر خط و دایره در دو نقطه مشترک باشند، می گوییم خط و دایره متقاطع اند.

در شکل مقابل، خط d دایره (C) را در دو نقطه A و B قطع رده است. در این حالت خط را نسبت به دایره قاطع می نامیم.

فاصله یک نقطه از یک خط در ریاضی

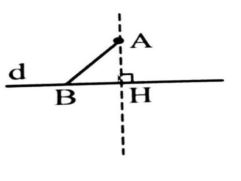
اگر از یک نقطه خارج یک خط، عمودی بر آن رسم کنیم، فاصله آن تا پای عمود، کوتاه ترین فاصله بین نقطه A و نقاط خط می باشد.

در شکل زیر، AH کوتاه ترین فاصله نقطه A تا نقاط خط d است (AB>AH) و به آن فاصله نقطه A تا خط d گفته می شود. اگر A روی خط d باشد، فاصله A تا خط d صفر است.

اوضاع نسبی یک خط و یک دایره هندسه یازدهم

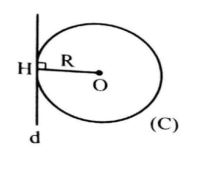
الف) خط بر دایره مماس است، اگر و تنها اگر فاصله مرکز دایره تا خط برابر شعاع دایره باشد.

OH=R  خط d و دایره (C) مماس است.

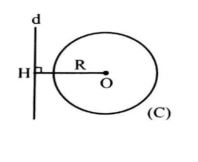
ب) خط با دایره متقاطع است، اگر و تنها اگر فاصله مرکز تا خط کمتر از شعاع دایره باشد.

OH<R خط d و دایره (C) متقاطع اند.

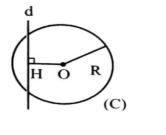
ج) خط و دایره نقطه اشتراکی ندارند، اگر و تنها اگر فاصله مرکز دایره تا خط، بزرگتر از شعاع دایره باشد.

OH>R  خط d و دایره (C) نقطه اشتراکی ندارند.

خاصیت مهم خط مماس

خاصیت 1- اگر A نقطه ای روی دایره باشد، شعاع OA و خط مماس بر دایره در نقطه A بر هم عمودند.

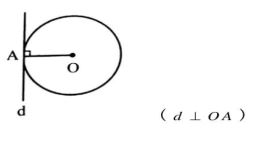
اثبات: فرض کنیم خط d در نقطه A بر دایره C(O,R) مماس باشد، از نقطه O عمود OH را بر خط d رسم می کنیم.

الف) اگر OH>R باشد، خط d بر دایره C متقاطع نیستند که با فرض مماس بودن خط d و دایره C تناقض دارد.

ب) اگر OH<R باشد، خط d و دایره C در دو نقطه متقاطع می شوند که با فرض مماس بودن آنها تناقض دارد.

ج) اگر OH=R باشد، در این صورت H روی دایره C قرار دارد و چون H روی خط d نیز هست، پس به جهت مماس بودن خط و دایره نتیجه می شود: H همان A است. بنابراین OA بر خط d عمود است.

چگونگی رسم خط مماس بر دایره در نقطه A بر دایره (به کمک خاصیت 1)

مرکز دایره را به نقطه A وصل می کنیم. سپس در نقطه A خط d را عمود بر OA رسم می کنیم. خط d در نقطه A بر دایره C مماس است.

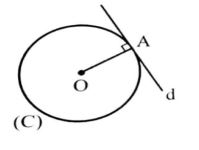
خاصیت 2- اگر خطی در انتهای شعاعی از دایره بر آن شعاع عمود باشد، آنگاه این خط بر دایره مماس است.

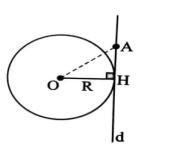
راه حل: در شکل بالا، خط d در نقطه ی H بر شعاع OHعمود است. باید ثابت کنیم خط d بر دایره مماس است. برای این کار کافی است ثابت کنیم خط d و دایره ی C(O,R) فقط در نقطه ی H مشترک اند.

فرض کنید نقطه A نقطه ای غیر از H و روی خط d باشد. چون مثلث OAH قائم الزاویه است و OA وتر آن است، پس OH<OA یعنی R<0. بنابراین A خارج دایره است. در نتیجه خط d و دایره فقط در یک نقطه ی H مشترک هستند و این نتیجه می دهد که خط d بر دایره مماس است.

نتیجه خاصیت 1 و 2: در صفحه یک خط و دایره بر هم مماس اند، اگر و تنها اگر این خط بر شعاع نقطه تماس عمود باشد.

تعاریف و مفاهیم اولیه هندسه یازدهم

الف) شعاع دایره: پاره خطی که یک سر آن مرکز دایره و سر دیگر آن نقطه ای روی دایره است.

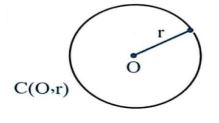
ب) وتر دایره: پاره خطی که دو نقطه ی متمایز از دایره را به هم وصل می کند. به عبارت دیگر پاره خطی که دو سر آن روی دایره باشد.

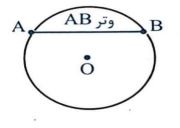
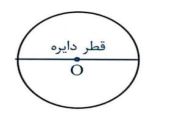
ج) قطر دایره: وتری از دایره که از مرکز دایره می گذارد.

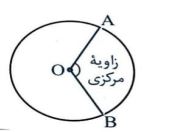
د) زاویه مرکزی: زاویه ای که رأس آن بر مرکز دایره واقع است.

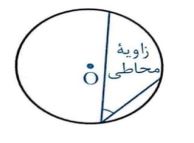
ه) زاویه محاطی: زاویه ای است که رأس آن روی دایره و اضلاع آن دو وتر از دایره باشند.

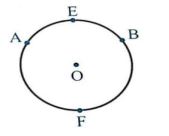
و) کمان: دو نقطه A و B واقع بر یک دایره دو کمان AB را روی آن دایره مشخص می کند. در این حالت برای مشخص کردن هر یک از آنها از نقطه ای اختیاری واقع بر هر یک از دو کمان استفاده می شود. مانند کمان های AEB و AFB در شکل زیر. معمولاً منظور از AB کمان کوچکتر است.

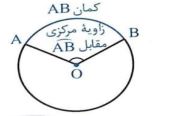
ز) اندازه کمان: هر یک از زاویه های مرکزی یک کمان از دایره جدا می شود به آن کمان، کمان نظیر آن زاویه مرکزی گفته می شود. اندازه کمان نظیر هر زاویه مرکزی، همان اندازه زاویه مقابل به آن کمان تعریف می شود که واحد آن درجه است.

تذکر: دقت کنید که نباید اندازه ی یک کمان را با طول آن اشتباه گرفت. برای درک این مطلب به شکل زیر دقت کنید:

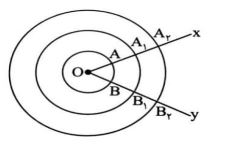
در این شکل سه دایره ی هم مرکز رسم کرده ایم. با توجه به مطلب بالا، اندازه کمان های AB، A₁B₁ و A₂B₂ برابرند. یعنی:

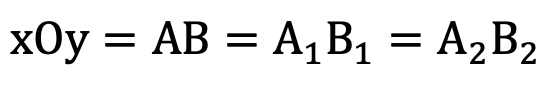
اما طول این کمان ها با هم برابر نیستند:

طول کمان A₂B₂> طول کمان A₁B₁> طول کمان AB

خواص وتر های مساوی در دایره

1) در یک دایره (یا دو دایره به شعاع های مساوی) دو وتر برابرند، اگر و تنها اگر کمان های نظیر آنها برابر باشند.

 

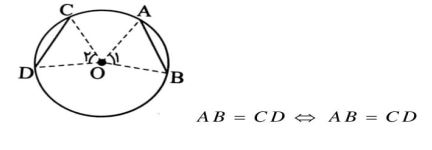
راه حل اثبات دو بخش دارد:

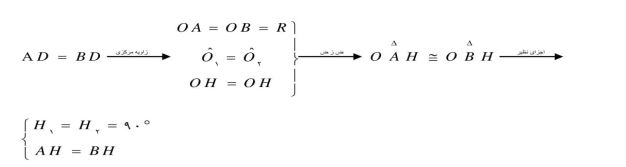
بخش اول: فرض می کنیم AB=CD و ثابت می کنیم AB=CD (به شکل دقت کنید) از مرکز دایره به دو سر وتر های AB و CD وصل می کنیم.

دو مثلث OAB و OCD به حالت تساوی سه ضلع هم نهشت اند:

 

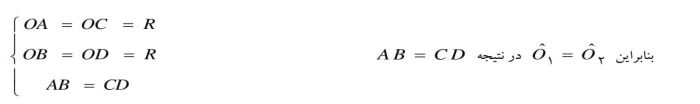
بخش دوم: فرض می کنیم AB=CD و ثابت می کنیم AB=CD

چون دو کمان AB و CD با هم برابرند، پس زاویه های مرکزی روبرو با آنها با هم برابرند، یعنی O ̂_1=O ̂_2

اکنون دو مثلث OAB و OCD به حالت تساوی دو ضلع و زاویه بین آنها با هم، هم نهشت اند:

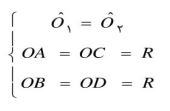
و در نتیجه AB=CD خواهد بود.

چگونه نصف شدن وتر بوسیله قطر دایره در هندسه یازدهم فصل اول

دایره ها نیز یکی از مضووعات اصلی هندسه یازدهم فصل اول است که باید به آن توجه داشت.

1- در هر دایره قطر عمود بر هر وتر آن وتر و کمان های نظیر آن وتر را نصف می کند.

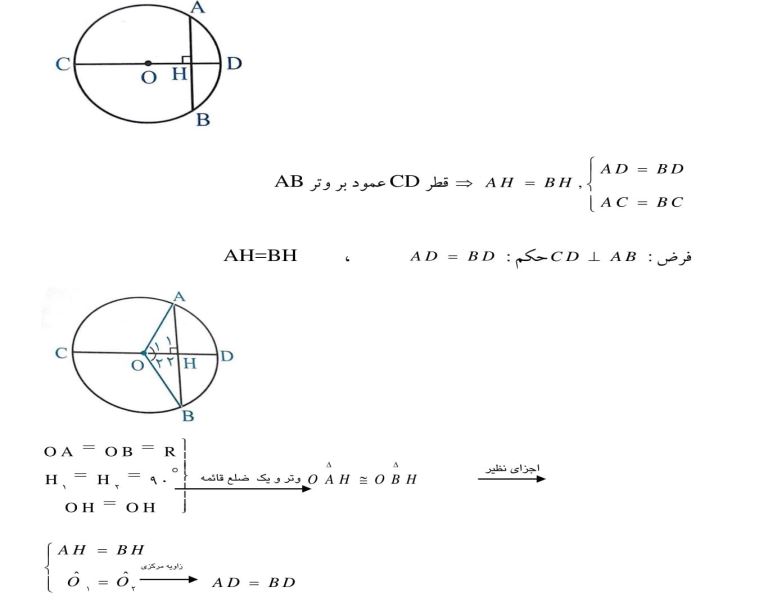
2- در هر دایره اگر قطری از آن یک وتر را نصف کند، آنگاه بر آن وتر عمود است و کمان های نظیر وتر را نصف می کند.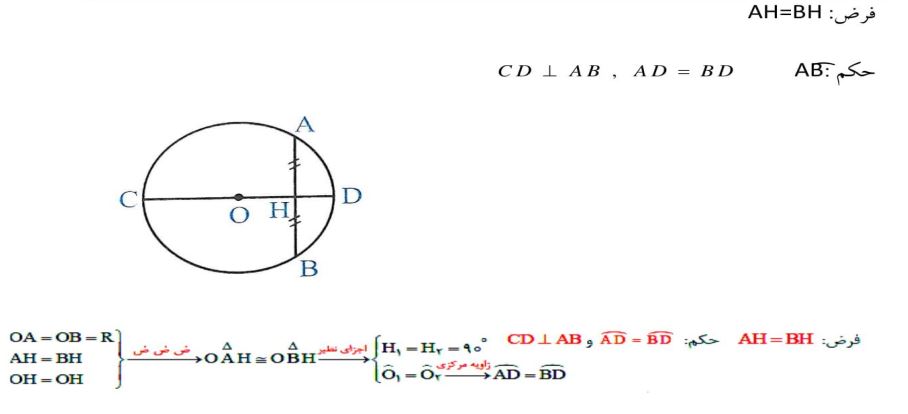

3- در هر دایره قطری از دایره که یک سر آن وسط کمان نظیر یک وتر باشد بر آن وتر باشد بر آن وتر عمود است و آن را نصف می کند.

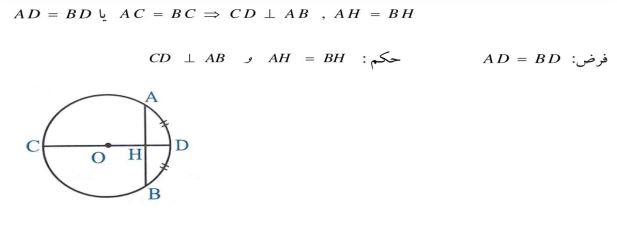
نتیجه: عمود منصف وتر دایره از مرکز دایره می گذرد.

همچنین ببینید: دوران و تقارن چرخشی در ریاضی

فاصله دو وتر مساوی از مرکز دایره

در یک دایره (یا دو دایره با شعاع های مساوی) دو وتر برابرند، اگر و تنها اگر فاصله مرکز دایره از آنها برابر باشد

AB=CD <=> OH=OH’

راه حل: فرض می کنیم AB=CD می خواهیم ثابت کنیم’ OH=OH و برعکس.

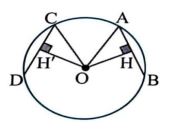
از نقطه ی O مرکز دایره، عمود های ’OH و OH را به ترتیب بر وتر های AB و CD رسم می کنیم. در دو مثلث قائم الزاویه ی OAH و OCH’ بنا بر قضیه فیثاغورث:

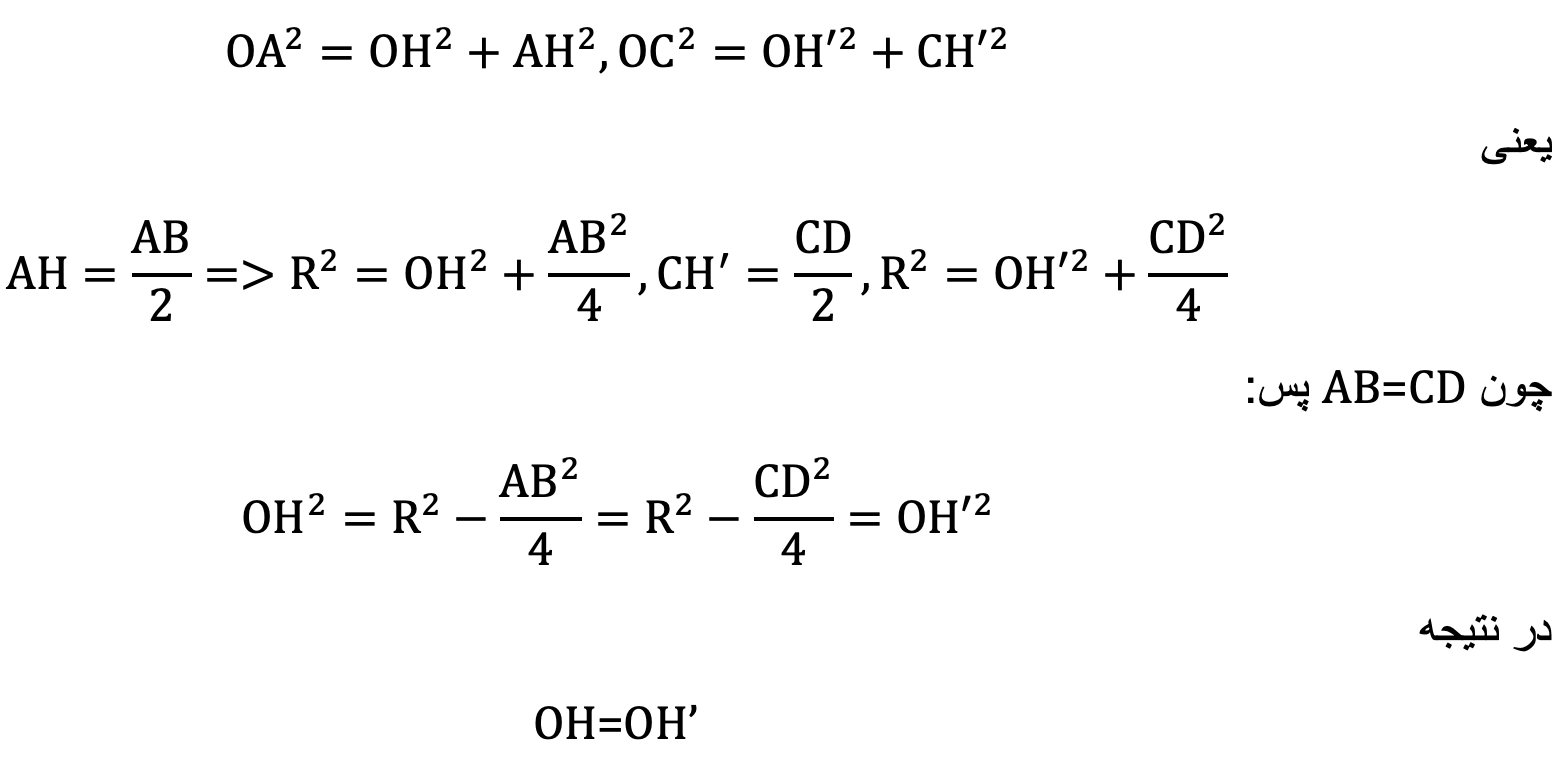
با عمل بازگشتی نیز می توان عکس این مطلب را ثابت کرد.

خواص وتر های نامساوی در دایره

در یک دایره اگر دو وتر نامساوی باشند، آنگاه وتری که بزرگتر است به مرکز دایره نزدیک تر است و بالعکس. به عبارت دیگر در دایره C(O,R)، AB>CD، اگر و تنها اگر OH<OH’ (OH و OH’ فاصله O از دو وتر AB و CD هستند).

برای درک بهتر این موضوع می توانید به تمرین 8 صفحه 18 کتاب درسی رجوع کنید.

زاویه محاطی و اندازه آن

زاویه محاطی: زاویه ای است که رأس آن روی دایره و اضلاع آن شامل دو وتر از دایره باشند. شکل زیر زاویه محاطی BAC را نشان می دهد:

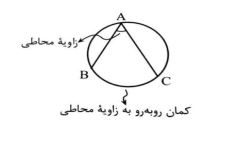
اندازه زاویه محاطی: اندازه هر زاویه محاطی برابر با نصف اندازه کمان روبرو آن است یعنی در هر سه حالت زیر داریم: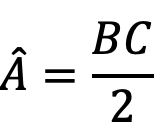

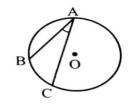
حالت اول: یک ضلع زاویه محاطی وتری از دایره باشد:

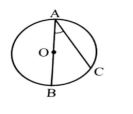
حالت دوم: دو ضلع زاویه محاطی در دو طرف مرکز قرار داشته باشند:

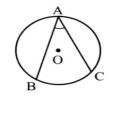
حالت سوم: دو ضلع زاویه محاطی در یک طرف مرکز باشند:

نتیجه:

1. در هر دایره اندازه زاویه های محاطی روبروی یک کمان، با هم برابرند
2. زاویه محاطی روبرو به قطر دایره 90⁰ است. چون قطر دایره، دایره را به دو کمان 90 درجه تقسیم می کند.

زاویه ظلی و اندازه آن در هندسه یازدهم

زاویه ظلی: زاویه ای است که رأس آن روی دایره می باشد یکی از اضلاع آن وتری از دایره و ضلع دیگرش مماس بر دایره است. مثل BAC در شکل زیر:

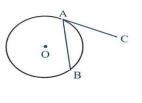
قضیه: اندازه هر زاویه ظلی، برابر نصف کمانروبروی آن است. یعنی :

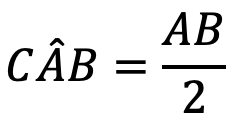
زاویه بین دو وتر در دایره

1) اگر مطابق شکل دو وتر AB و CD در نقطه M متقاطع باشند، آنگاه:

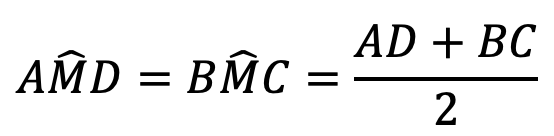
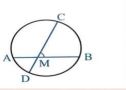
2) اگر مطابق شکل امتداد دو وتر AB و CD یکدیگر را در نقطه M قطع کنند، آنگاه:

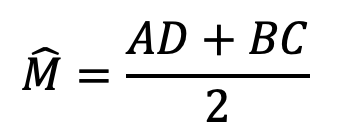
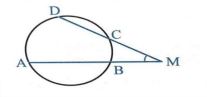
زاویه بین دو مماس در هندسه

اگر مطابق شکل از نقطه M دو مماس بر دایره رسم شود، آنگاه زاویه بین دو مماس برابر است:

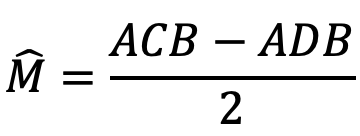
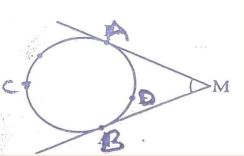
زاویه بین مماس و امتداد یک وتر

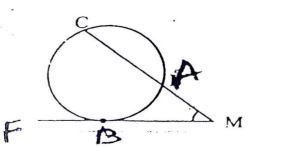
اگر مطابق شکل، امتداد وتر BC و خط مماس بر دایره در نقطه A یکدیگر ار در نقطه M قطع کنند، آنگاه:

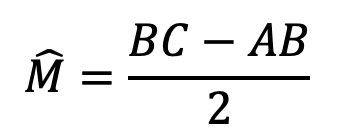
همچنین برای فصل های بعدی میتوانید قضیه تالس را نیز مشاهده نمایید.

---