نحوه محاسبه معادلات مثلثاتی و کاربرد آن

امروزه ریاضیات و مباحث معادلات مثلثاتی جز مباحث و علومی است که در بسیار حوزه ها نقش داشته و از آن استفاده های فراوانی می شود. کاربرد معادلات مثلثاتی با بسط دادن فرمول ها، گسترش یافته و میتوان معادلات جدیدی را از آن استخراج نمود. تاریخچه معادلات مثلثاتی بسیار کهن و دیرینه بوده ولی با این حال امروزه نیز مورد استفاده می باشد. در این مباحث شما با روش های به دست آوردن اندازه یک زاویه از طریق روابط سینوس و کسینوس را آموخته همچنین میتوانید با داشتن یک زاویه، دو برابر سینوس کسینوس و یا معکوس آن زاویه را به دست اورید. معمولا از روابط مثلثاتی و دایره مثلثاتی و با استفاده از رابطه فیثاغورث میتوان طول یک مسیر، و یا اندازه زاویه آن را به راحتی تعیین کرد.

دایره مثلثاتی:

همیشه مباحث ریاضیات برای بسیاری از دانش آموزان سخت و غیر قابل فهم بوده و دانش آموزان نیاز داشتند تا تلاش بیشتری کنند تا انواع معادلات و روابط ریاضی را درک کنند. معادلات مثلثاتی جز مباحثی از ریاضیات می باشد که معمولا از آن برای درک بهتر مفهوم کسینوس و سینوس استفاده می شود. دایره مثلثاتی دایره ای به شعاع 1 می باشد که با استفاده از دایره و مثلثی که در داخل این دایره رسم می شود می توان روابط سینوس و کسینوس را را به راحتی به خاطر سپرد. اگر درون دایره یک خط افقی و یک خط عمودی رسم کنیم، دایره به چهار ربع مساوی تقسیم خواهد شد. محور عمودی بیانگر سینوس و محور افقی بیانگر کسینوس خواهد بود. با این حساب در ربع اول علامت های سینوس و کسینوس به صورت زیر خواهد بود. در ربع اول سینوس مثبت و کسینوس منفی، در ربع دوم سینوس مثبت و کسینوس منفی، در ربع سوم سینوس و کسینوس منفی و در ربع چهارم سینوس مثبت و کسینوس منفی می باشد.

حرکت بر روی این دایره به صورت پادساعتگرد می باشد. برای محاسبه اندازه یک زاویه ابتدا آن را بر روی دایره مشخص کرده و از مرکز دایره به آن نقطه پاره خطی را رسم میکنیم سپس برای بدست آوردن سینوس، این نقطه را به محور سینوس و برای به دست آوردن کسینوس این نقطه را به محور کسینوس عمود می کنیم. با توجه به اینکه شعاع برابر یک می باشد می توان از قانون فیثاغورث برای به دست آوردن سینوس و یا کسینوس زاویه مورد نظر استفاده کرد.

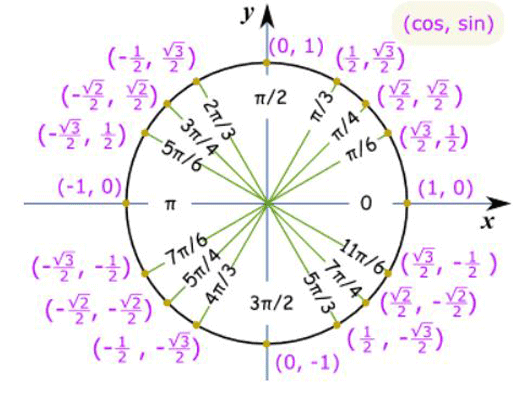
نسبت مثلثاتی و دایره مثلثاتی:

از روابط مثلثاتی میتوان برای به دست آوردن اندازه تمام زاویه ها، محاسبه تابع و معادلات مثلثاتی و یا جمع و تفریق دو زاویه استفاده کرد. در معادلات مثلثاتی اینکه انتهای کمان در کدام ربع از دایره قرار میگیرد مهم می باشد، زیرا تعیین کننده علامت نسبت های مثلثاتی خواهد بود. دایره مثلثاتی، دایره ای است روی محور مختصات به مرکز (0,0) و شعاع 1. به عبارتی دایره محور مختصات را در نقطه های(0,1) و (1,0) و (0 ,1-) و (1- , 0) قطع می کند. برای به دست آوردن اندازه یک زاویه با استفاده از دایره و معادلات مثلثاتی، پس از رسم آن زاویه بر روی دایره و عمود کردن خطی از نقطه مشخص شده، به محور های x , y و به دست آوردن یک مثلث قائم الزاویه که وتر آن برابر شعاع دایره و برابر مقدار 1 است، می توان حاصل زاویه را از طریق محاسبات زیر به دست آورد. سینوس یک زاویه برابر با تقسیم اندازه ضلع روبروی زاویه مورد نظر به اندازه وتر می باشد. همچنین کسینوس برابر تقسیم اندازه ضلع مجاور زاویه به اندازه وتر می باشد.

نحوه محاسبه کسینوس و سینوس زاویه در معادلات مثلثاتی:

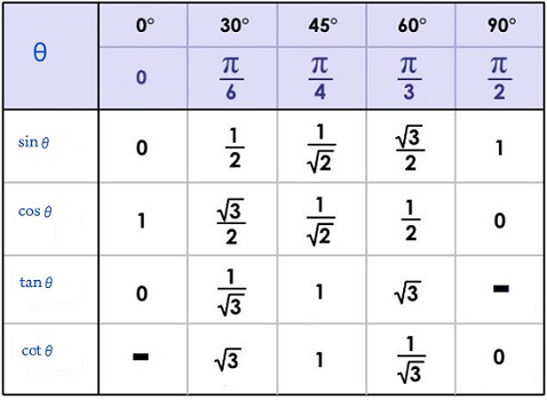
تابع کسینوس و سینوس، تابعی تناوبی بوده و می توان آنها را بر روی مختصات دکارتی رسم کرد. برای محاسبه و اندازه گیری سینوس و کسینوس یک زاویه می توان با استفاده از دایره و معادلات مثلثاتی آن را به دست آورد. برخی از زوایای پر کاربرد مثل 30 درجه، 60 درجه، 90 درجه، 180 درجه، 270 درجه و 360 درجه یا به عبارتی 0 درجه، در جدول زیر محاسبه شده و قرار داده شده است. شما میتوانید با به خاطر سپردن مقادیر این زوایا از آنها برای به دست آوردن مقادیر دیگر زوایا استفاده کنید. زوایا را میتوان بر حسب درجه و یا رادیان محاسبه نمود. برای مثال 2/π بر حسب رادیان برابر 90 درجه می باشد. میتوانید با تبدیل رادیان به درجه و یا برعکس، سینوس و کسینوس برخی از زوایا را نیز به دست آورید.

معکوس نسبت مثلثاتی:

تاریخچه معادلات مثلثاتی بسیار دیرینه بوده و در گذشته از این علم در نجوم استفاده می شد که بعدها توسط ناصر الدین طوسی، این مبحث به عنوان یک مبحث مستقل از نجوم و به عنوان شاخه ای از ریاضی در نظر گرفته شد. معمولا از توابعی نظیر کسینوس، سینسوس، تانژانت و کتانژانت برای برقراری یک رابطه بین زوایا و طول یک مثلث استفاده می شود که این معادلات مثلثاتی کاربرد فراوانی در حوزه های مختلفی دارد. نحوه محاسبه سینوس و کسینوس در بالا شرح داده شد. برای محاسبه تانژانت از تقسیم ضلع مقابل به مجاور و برای به دست آوردن کتانژانت از تقسیم اندازه ضلع مجاور به مقابل استفاده می شود. از این روابط برای به دست آوردن مقدار یک زاویه استفاده می شد. روابط تانژانت و کتانژانت که معکوس یکدیگر بودند. از این رو میتوان معکوس سینوس و کسینوس را نیز به دست آورد که به ترتیب با نام های کسکانت و سکانت شناخته می شوند. سکانت برابر یک تقسیم به سینوس تتا و کسکانت برابر یک تقسیم بر کسینوس تتا می باشد.

ببینید: دامنه و برد تابع

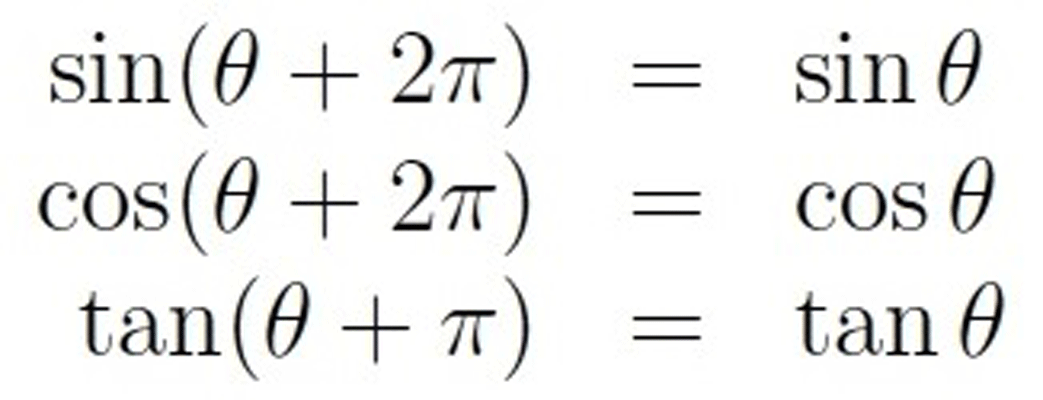
نسبت مثلثاتی برای مجموع زاویه‌ها:

شما به راحتی می توانید با بسط دادن یک فرمول، معادلات پرکاربرد دیگری را به دست آورید. شما میتوانید با استفاده از نسبت مثلثاتی برای مجموع زاویه‌ها به راحتی می توانید سینوس، کسینوس و یا تانژانت زاویه هایی را که نمی دانید را به دست آورید. برای مثال اگر شما نیاز به بدست آوردن سینوس زاویه 75 درجه را دارید، می توانید این زاویه را به دو زاویه 30 درجه و 45 درجه تقسیم کنید. زیرا در این حالت شما اندازه این دو زاویه پرکاربرد را به خاطر دارید و با استفاده از فرمول نسبت مثلثاتی برای مجموع زاویه‌ها میتوانید به راحتی آن را محاسبه کنید. همچنین می توانید با داشتن فرمول های تبدیل ضرب به جمع و نیز برعکس، زاویه ها را به یکدیگر تبدیل کرده و معادلات جدیدی را به دست آورید.

کاربرد معادلات مثلثاتی در حوزه های دیگر:

معادلات مثلثاتی و ریاضیات از زمان های قدیم برای حل بسیاری از مسائل مورد استفاده بوده است. معادلات مثلثاتی را میتوان گفت پرکاربردترین مبحث ریاضیات می باشد که از ان در حوزه های برق، نقشه برداری، مکانیک، عمران و سایر حوزه ها استفاده فراوانی می شود. از این مبحث در نجوم و ستاره شناسی، جهت یابی و تعیین موقعیت جغرافیایی که امروزه در هوش مصنوعی و سیستم موقعیت یابی جهانی نیز از آن استفاده میشود، در حوزه تولید صوت و موسیقی، لرزه شناسی، هواشناسی، گرافیک رایانه ای، اقیانوس شناسی، سی تی اسکن، هندسه، معماری و نیز الکترونیک از آن استفاده می شود.

 در صورتی که علاقه مند به یادگیری هندسه هستید هندسه یازدهم فصل اول را نیز مشاهده کنید