فیلم آموزش لگاریتم

یکی از علت های ایجاد لگاریتم را می توان ساده کردن عملیات ضرب معرفی کرد. همچنین گرفتن لگاریتم از اعداد مختلف، مقیاس اعداد را کوچک تر می کند که با توجه به این موضوع می توان نتیجه گرفت که لگاریتم به جهت ساده سازی عملیات ریاضی با مقادیر بزرگ بوجود آمده است.

تاریخچه لگاریتم در ریاضی

جان نِپِر (John Napier) دانشمند اسکاتلندی در سال 1614 کلمه لگاریتم را برای عملگر ابداعی خود به کار گرفت، به این صورت که عملگر، عکس عمل توان یا همان ضرب بصورت متوالی، مورد محاسبه قرار می گرفت. قبل از نِپِر، دانشمندان دیگری نیز در زمینه لگاریتم و خصوصیات آن فعالیت هایی داشتند اما برای نخستین بار نِپِر موفق به استفاده از آن شد. معمولاً تعریفی که از لگاریتم در ریاضیات می شود، ساده کردن حاصل ضرب توان هایی از عدد 10 است. در نتیجه لگاریتم را بر مبنای 10 قرار می دهند. این نکته را در نظر داشته باشید که اگر ضرب ها را بر مبنای عدد دیگری در نظر بگریم، مبنای لگاریتم نیز تغییر خواهد کرد.

فیلم آموزش لگاریتم

آموزش لگاریتم به زبان ساده

نکته: عدد e را عدد نِپِر می گوییم و مقدار آن 7/2 است. پس  همواره صعودی خواهد بود.

نکته: یادتان باشد با توجه به ارتباطی که توان و لگاریتم با یکدیگر دارند، اعداد منفی لگاریتم نخواهند داشت.

برای درک بهتر مفهوم لگاریتم به مثال های زیر توجه کنید.

مثال 1) عدد 100 را می توان به صورت ضرب عدد  نوشت:

100=10×10=10^2

تعداد ضرب هایی از عدد 10 که منجر به عدد 100 می شود، برابر با 2 می باشد. بنابراین خواهیم داشت:

log_10⁡〖(100)〗=2

واضح است که در این مثال مبنای لگاریتم ما عدد 10 است که بصورت اندیس در زیر عملگر لگاریتم (log) نوشته می شود. پس با توجه به این موضوع می گوییم، لگاریتم عدد 100 بر مبنای 10 برابر است با 2.

در صورت نیاز به فیلم: قضیه تالس کلیک کنید

نکته: لگاریتم هر عدد بر مبنای خودش برابر با 1 خواهد بود به این علت که تساوی زیر برای هر عدد مثبتی برقرار است:

به عنوان مثال لگاریتم 10 بر مبنای 10، 1 می باشد.

مثال 2) عدد 32 ا می توان به صورت ضرب مولی اعداد 2 نوشت:

32=2×2×2×2×2=25

عمل ضرب عدد 2، به تعداد 5 مرتبه انجام گرفته است. پس با توجه به این موضوع می توانیم بگوییم، لگاریتم عدد 32 بر مبنای 2 برابر است با 5:

log_2⁡32=5

مثال 3) عدد  را در نظر داشته باشید. همانطور که قبلاً اشاره کردیم e4 عدد نِپِر است و زیر مجموعه اعداد گنگ (اصم) می باشد با معادل تقریبی 2/7182. پس با در نظر گرفتن این موضوع می توانیم بگوییم، لگاریتم عدد  بر مبنای e4 برابر با 4 است:

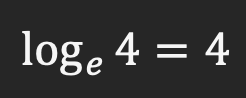
لگاریتم بر مبنای e را ln نیز می نامند که می توان تساوی بالا را بصورت زیر نیز نوشت:

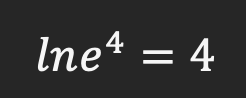
همانطور که مشاهده می کنید عملگر ln فقط برای مبنای عدد e است و برای دیگر مبنا ها نوشته نمی شود.

نکته: بعضی اوقات به مبنای لگاریتم، پایه لگاریتم هم گفته می شود به این علت که مبنای لگاریتم معادل پایه در تابع نمایی است. در مثال 1، عدد 10 به عنوان پایه توان 10 به توان 2 شناخته می شود و همچنین مبنا یا پایه لگاریتم 100، log_10⁡(100).

مثال 4) لگاریتم 150 بر مبنای 2 و 3 برقرار است چونکه رابطه زیر بین توان های 10 برقرار خواهد بود:

بنابراین

مثال 5) برای اعداد کوچکتر از یک، لگاریتم منفی خواهد بود. مثلاً لگاریتم ۱ به روی ۲ بصورت زیر محاسبه می شود:

به این دلیل که:

رابطه معکوس لگاریتم

همان طور که در ابتدا اشاره کردیم عمل به توان رساندن با لگاریتم ارتباط دارد و بنا بر تعریفی که از لگاریتم به زبان آوردیم ارتباط بین توان و لگاریتم را می توانیم بصورت زیر نمایش دهیم:

رابطه بالا به این معناست که کیب دو تابع لگاریتم و نمایی، یک تابع همانی خواهد بود. در واقع نشان دهنده این است که تابع لگاریتم، معکوس تابع نمایی می باشد و همچنین تابع نمایی، معکوس تابع لگاریتم به حساب می آید.

همچنین ببینید: آموزش تعیین علامت در ریاضی

رابطه بین ضرب و جمع در لگاریتم و خصوصیات آن

با در نظر گرفتن ارتباط بین عملگر های توان و لگاریتم می توانیم خصوصیاتی که برای توان در نظر می گیریم را به لگاریتم هم بسط دهیم. فرض بگیرید دو عدد به نام A و B داریم که می توانیم هر کدام از آنها را بصورت زیر تعریف کنیم:

A=ax, B=ay

بنابراین ضرب این دو عدد بصورت زیر خواهد بود:

به این دلیل که پایه تمامی این توان ها، برابر است، مبنای لگاریتم را نیز می توان a در نظر گرفت:

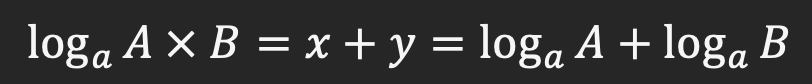
بنابراین می توانیم نتیجه بگیریم که:

لگاریتم حاصلضرب دو عدد، برابر است با حاصل جمع لگاریتم آنها

مثال 6) لگاریتم عدد 243 بر مبنای 3 را می توانیم با توجه به حاصلضرب اعداد 3 و 9 بنویسیم:

مثال 7) لگاریتم عدد 16 بر مبنای 2 را می توانیم به شکل زیر بنویسیم:

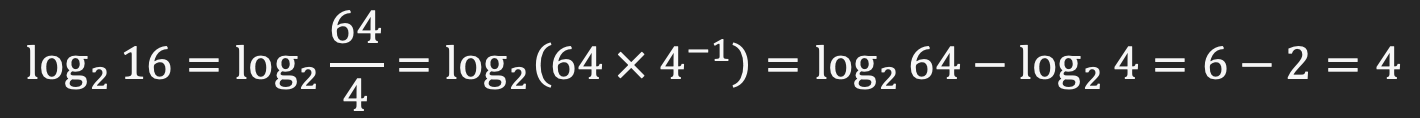
همانطور که می بینید لگاریتم تقسیم دو عدد بصورت تفاضل لگاریتم مخرج از صورت محاسبه خواهد شد. در نتیجه لگاریتم و خصوصیات آن در خصوص ضرب و تقسیم را نیز مورد بررسی قرار دادیم.

لگاریتم تقسیم دو عدد یا یک کسر، برابر است با، لگاریتم عدد صورت منهای لگاریتم عدد مخرج کسر

رابطه توان و جذر در لگاریتم و خصوصیات آن

A را به نوان یک عدد مثبت در نظر بگیرید که به توان p رسیده است. لگاریتم Ap  بر مبنای b بصورت زیر قابل نمایش است( p را یک عدد طبیعی در نظر بگیرید):

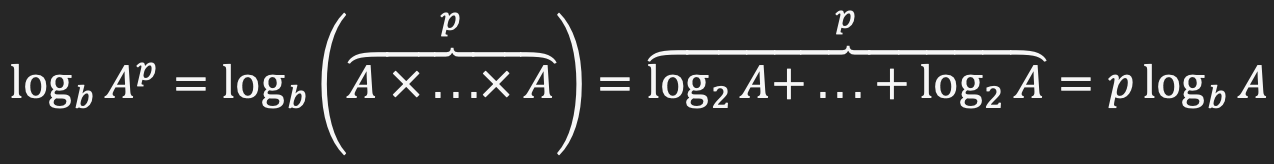
مثال 8) لگاریتم 64 بر مبنای 2 بصورت زیر محاسبه می شود:

در نظر داشته باشید  که بین توان و جذر نیز رابطه وجود دارد و برای درک بهتر این موضوع طبق مثال زیر می توانید لگاریتم جذر یک عدد را بدست آورید.

مثال 9) لگاریتم ریشه دوم 1000 برابر با 5/1 خواهد شد:

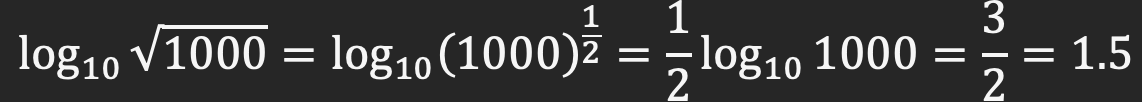
بنابراین با توجه به رابطه بالا می توان گفت:

لگاریتم توان یک عدد برابر است با حاصلضرب توان در لگاریتم آن عدد

در جدول زیر خصوصیات ضرب، تقسیم، توان و ریشه لگاریتم اعداد، خلاصه سازی شده است:

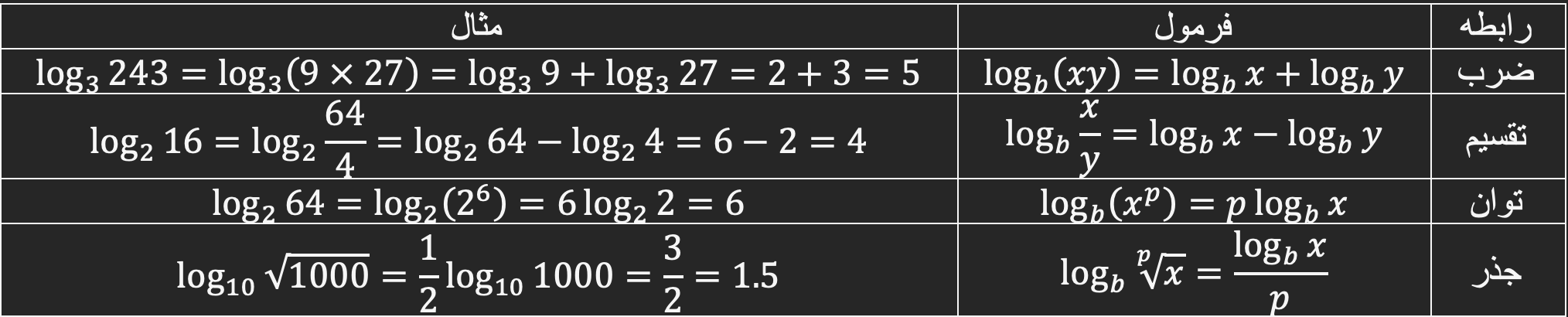
تغییر مبنا در لگاریتم و خصوصیات آن

بعضی اوقات در محاسبه لگاریتم، نیاز دارید که مبنای آن را تغییر دهید. از رابطه زیر برای تغییر مبنای لگاریتم x از b به k استفاده می کنیم:

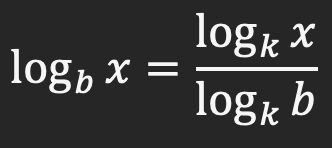
برای درک بهتر این رابطه، فرض کنید لگاریتم x بر مبنای b برابر با مقدار y باشد:

در نتیجه:

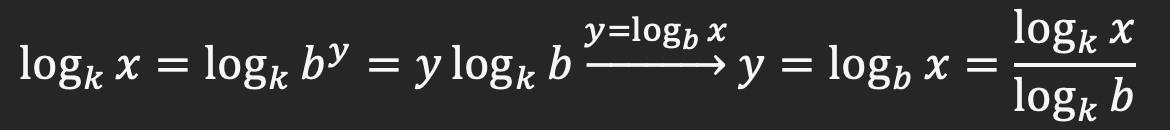
با توجه به رابطه بالا می توانیم لگاریتم یک عدد را بر مبنای عدد 10 یا لگاریتم طبیعی نیز از طریق رابطه زیر بدست آوریم:

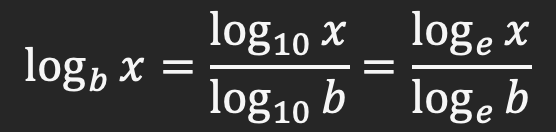
مثال 11) لگاریتم عدد 100 بر مبنای نامشخص برابر است با 2، در نتیجه می توانیم با توجه به رابطه بالا مبنا را بدست آوریم:

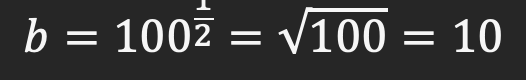
تابع لگاریتم و خصوصیات آن

تابع f(x) به عنوان لگاریتم یک عدد مثبت در نظر گرفته شده است. همانطور که مشاهده می کنید این تابع، مقادیر مثبتی از اعداد حقیقی خواهد بود و با توجه به نحوه محاسبات لگاریتم، برد تابع نیز زیر مجموعه ای از اعداد حقیقی خواهد بود. زیرا:

نمودار لگاریتم

نمودار تابع لگاریتم بر اساس مبنا های مختلف نیز به شکل زیر است:

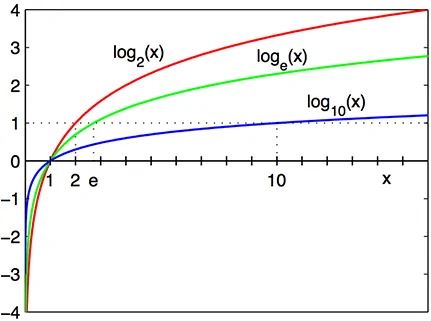
طبق نمودار، هنگامی که مقدار روی محور x ها (افقی)، از یک کوچکتر باشد، مقدار لگاریتم (روی محور y (عمود)) منفی می شود. در واقع تابع لگاریتم یک تابع مقعر محسوب می شود درست بر خلاف تابع نمایی که تابعی محدب است. که همانطورکه اشاره کردیم تابع لگاریتم را به عنوان معکوس تابع نمایی معرفی می کنند.

تابع لگاریتم با توجه به نمودار هایی که رسم شده است تابعی صعودی از x خواهد بود اگر مبنای بزرگتر از 1 داشته باشد:

نکته: اگر جای مبنا و متغیر را در لگاریتم عوض کنیم، مقدار لگاریتم معکوس می شود:

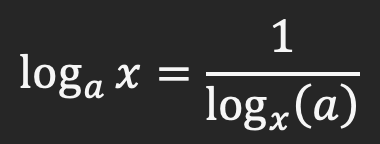
اگر فرض را بر این بگیریم که log_a⁡ x=A وlog_x⁡ a=B ، رابطه های زیر برقرار خواهند بود:

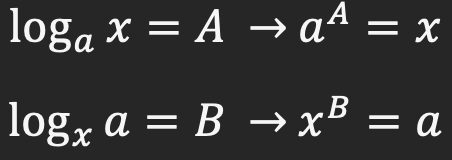
aA  ×  xb=x ×  a

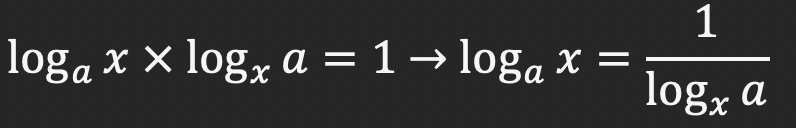
همچنین مهندس امیر محمودزاده یک جزوه بسیار بسیار دقیق و هوشمند برای بخش لگاریتم تهیه کرده. در صورت نیاز به دانلود جزوه لگاریتم اینجا کلیک کنید.