فصل سوم هندسه یازدهم
با شما هستیم با معرفی فصل سوم هندسه یازدهم و تمامی سرفصل های آن را به صورت خلاصه و روان توضیح خواهیم داد ناگفته نماند در دوره جامع ریاضی یازدهم تمامی این موارد گفته شده است.
یادآوری: روابط طولی در مثلث قائم الزاویه که در سال گذشته با آنها آشنا شده اید، عبارتند از:
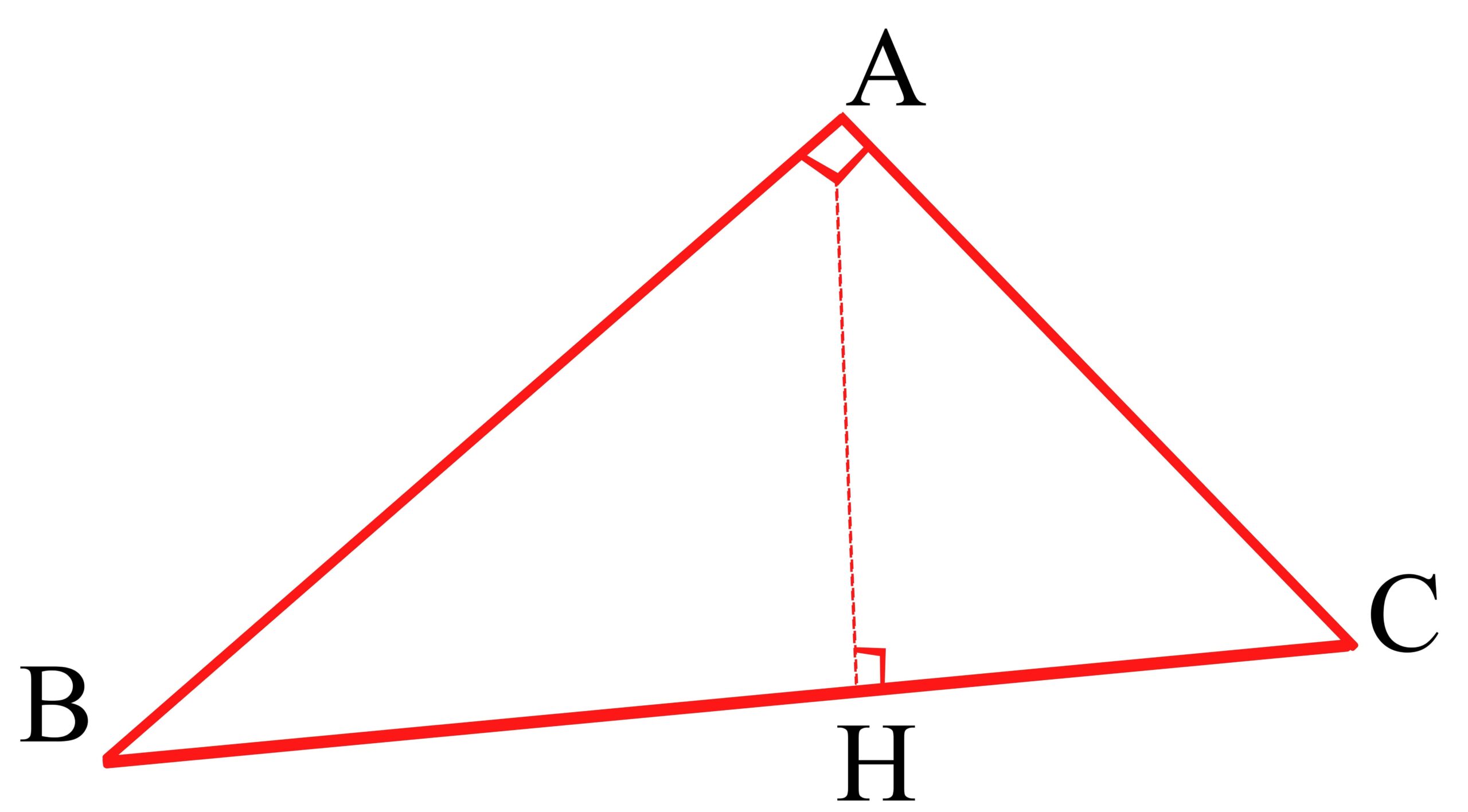
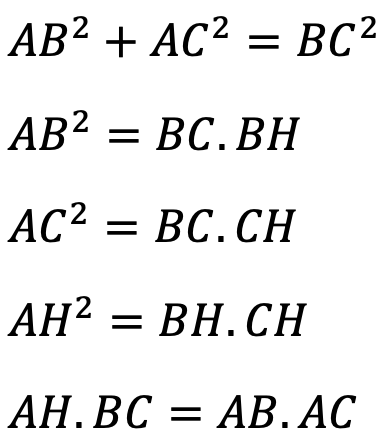
روابط طولی در مثلث
![]()
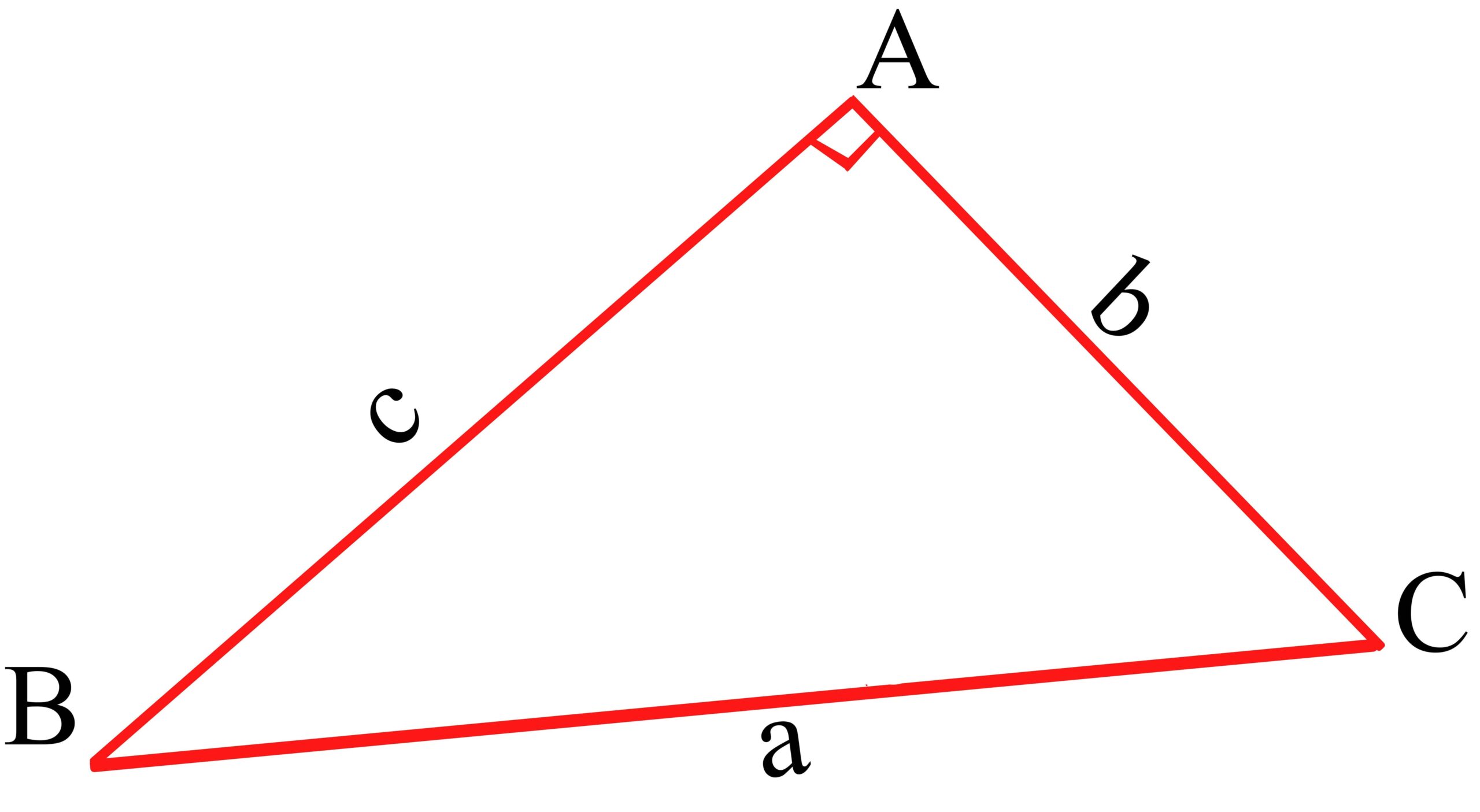
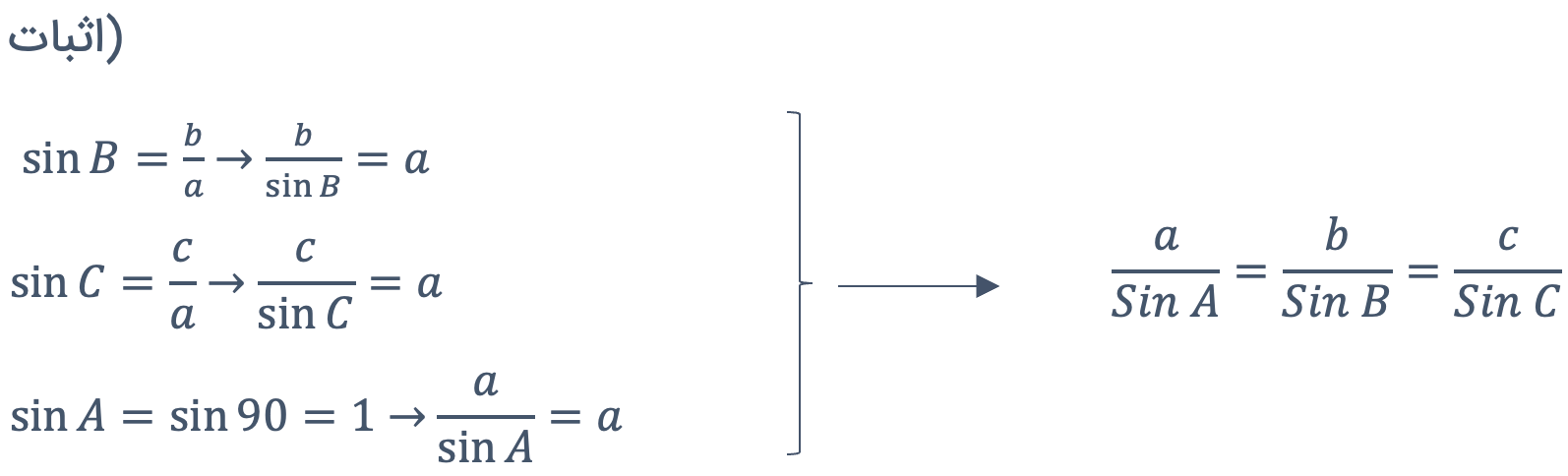
یادآوری: در هندسه ی دهم ثابت کردیم که عمود منصف های اضلاع هر مثلث، در یک نقطه هم رأس هستند همچنین در کتاب هندسه یازدهم نیز دیدیم که این نقطه ی هم رأسی، مرکز دایره محیطی مثلث است. حال اگر دایره محیطی مثلث قائم الزاویه را رسم کنیم، مشاهده می کنیم مرکز این دایره بر روی وتر مثلث قائم الزاویه است و لذا قطر دایره برابر است با وتر مثلث.
نتیجه: با توجه به مطالب بالا (در مثلث قائم الزاویه) خواهیم داشت:
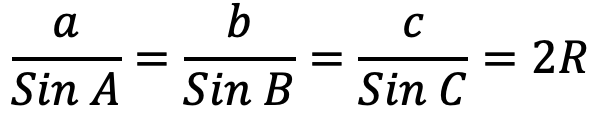
قضیه سینوس ها در هندسه
در قضیه سینوس ها، می خواهیم رابطه ی فوق را برای هر مثلث دلخواهی اثبات کنیم.
در هر مثلث ABC که AB=c، AC=b و BC=a باشد خواهیم داشت:
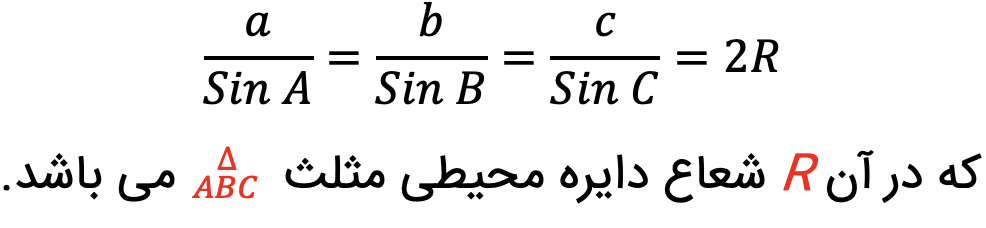
اثبات) مثلث ABC را در حالت های مختلف زیر بررسی می کنیم:
حالت اول – A=90 (رابطه فوق برای این حالت اثبات شده است)
مثلث ABC را رسم می کنیم. سپس قطر BD را مطابق شکل رسم کرده و D را به A وصل می کنیم:
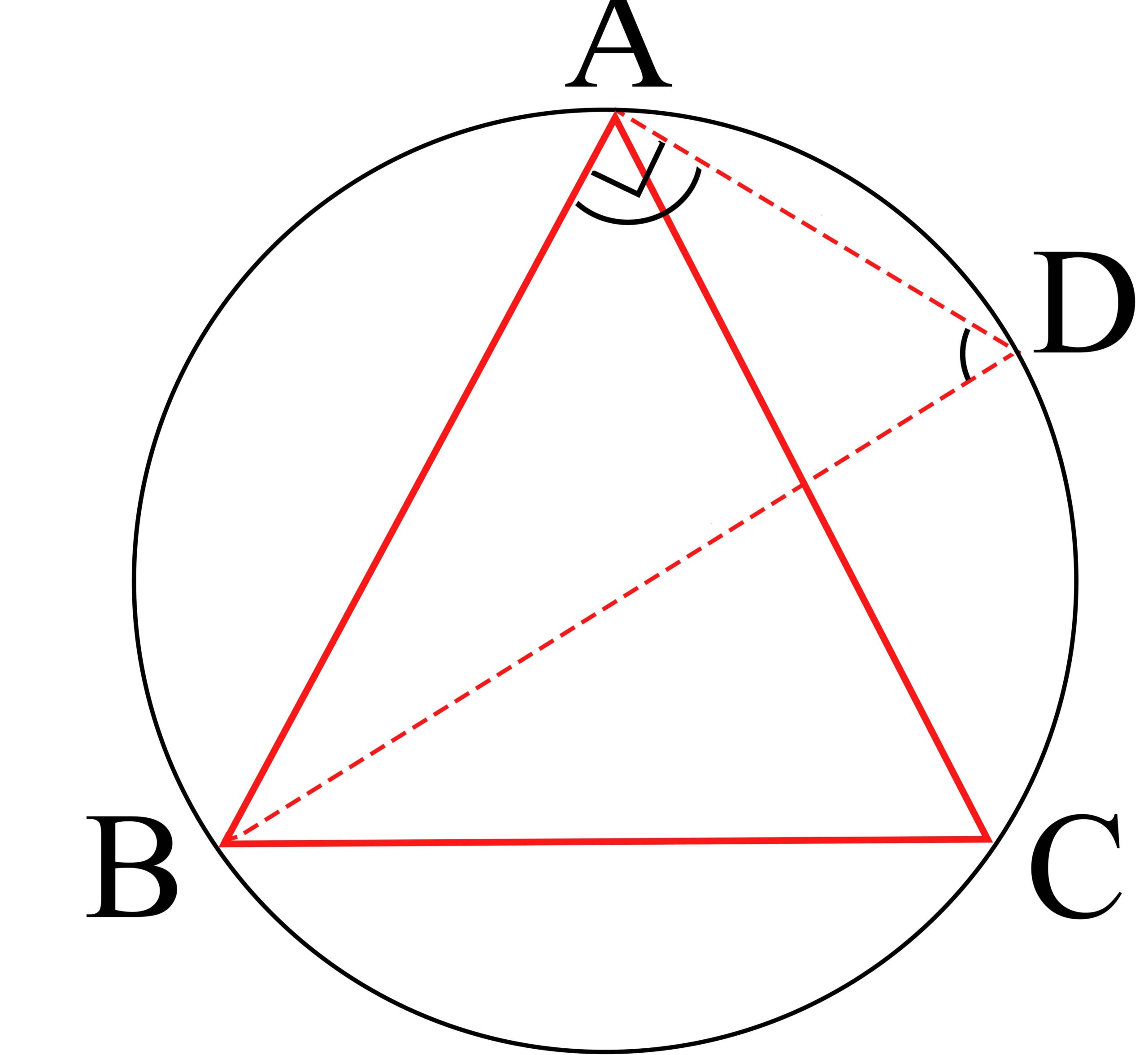


قضیه کسینوس ها در هندسه یازدهم
حالت اول A=90 می باشد که در این حالت مثلث ABC، قائم الزاویه است و لذا از قضیه فیثاغورس خواهیم داشت:
![]()
و چون cos 90 = 0 می باشد، ذا حکم بدست می آید:
![]()
حالت دوم A>90 خواهد بود:
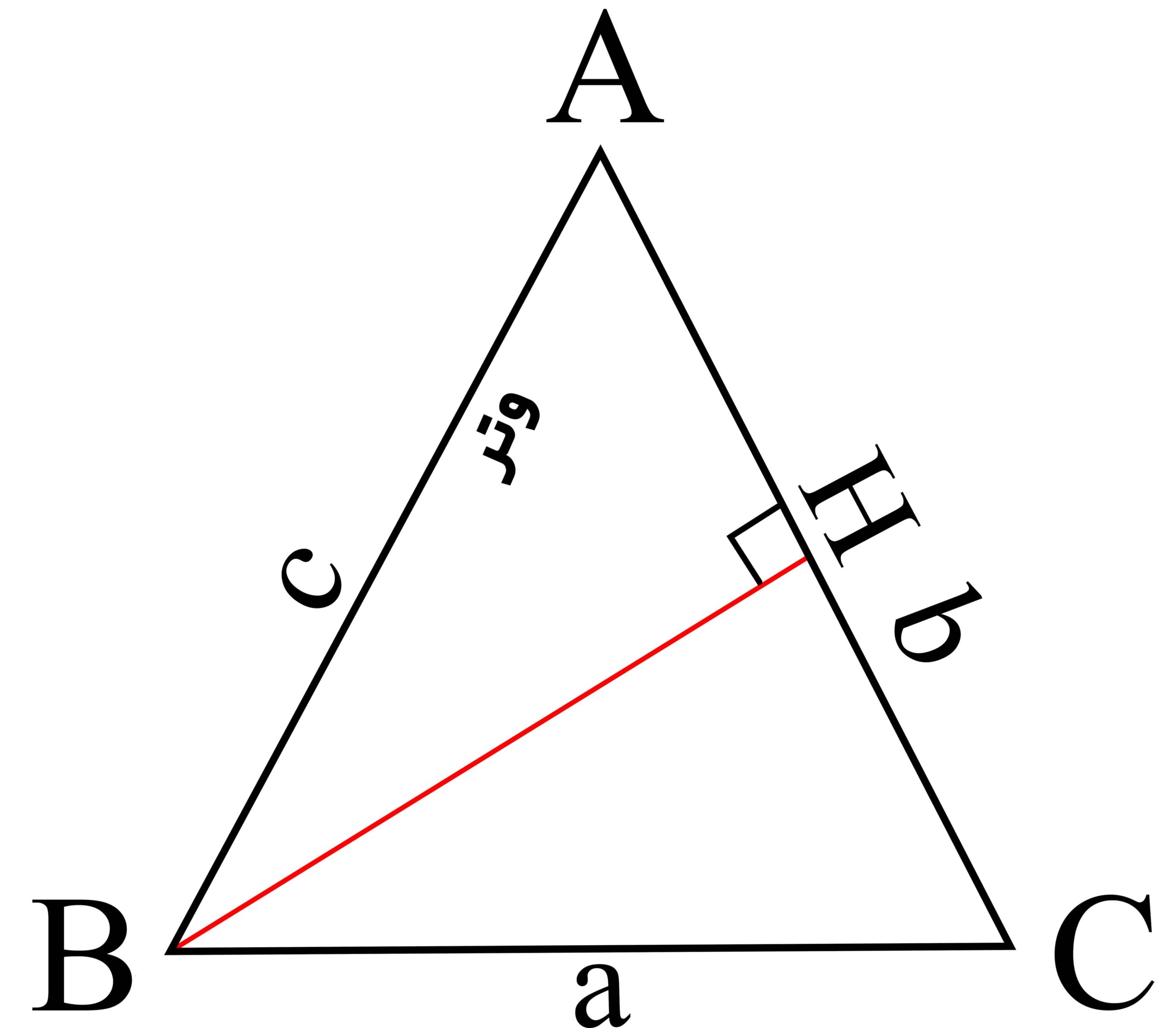
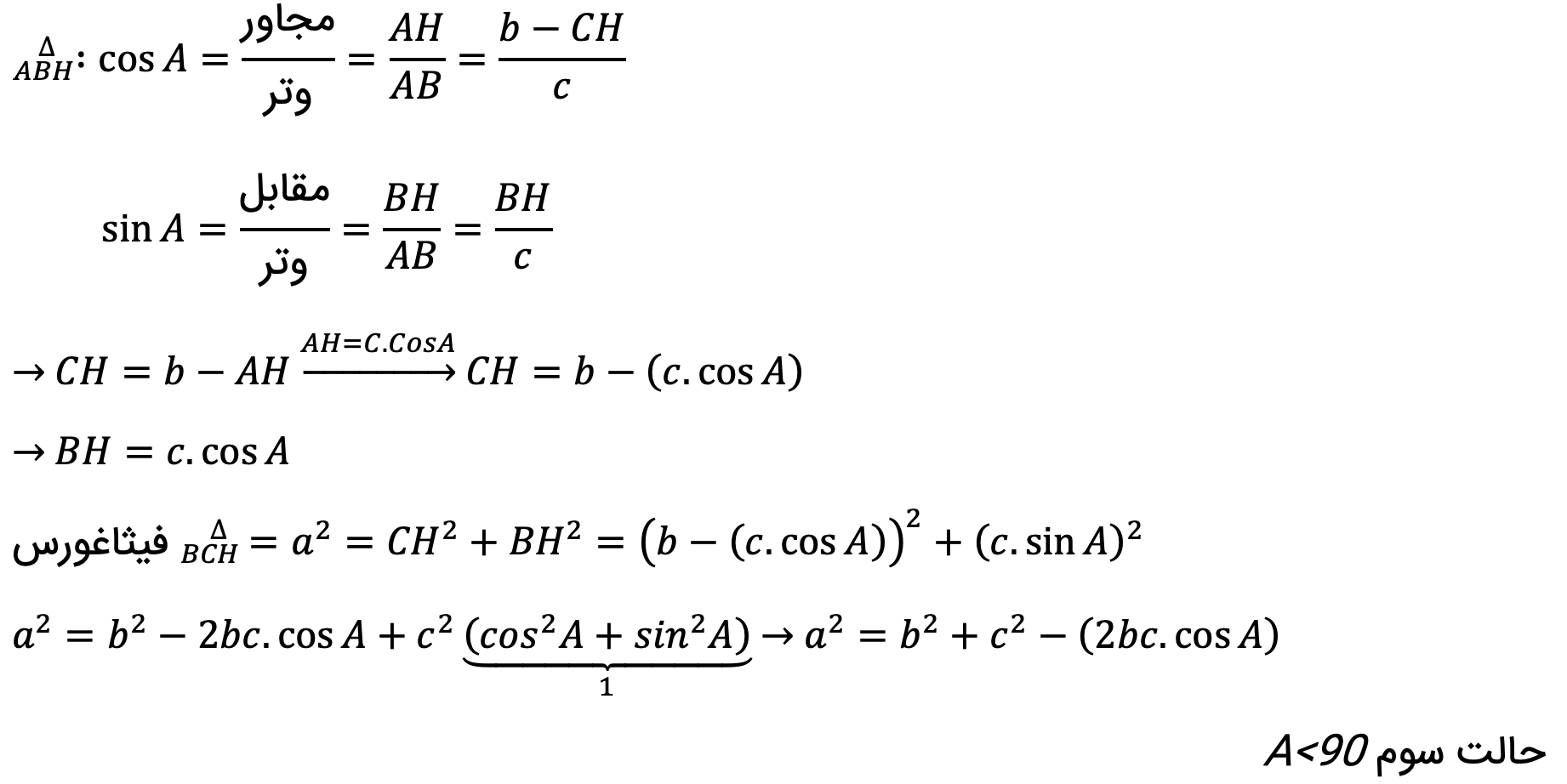
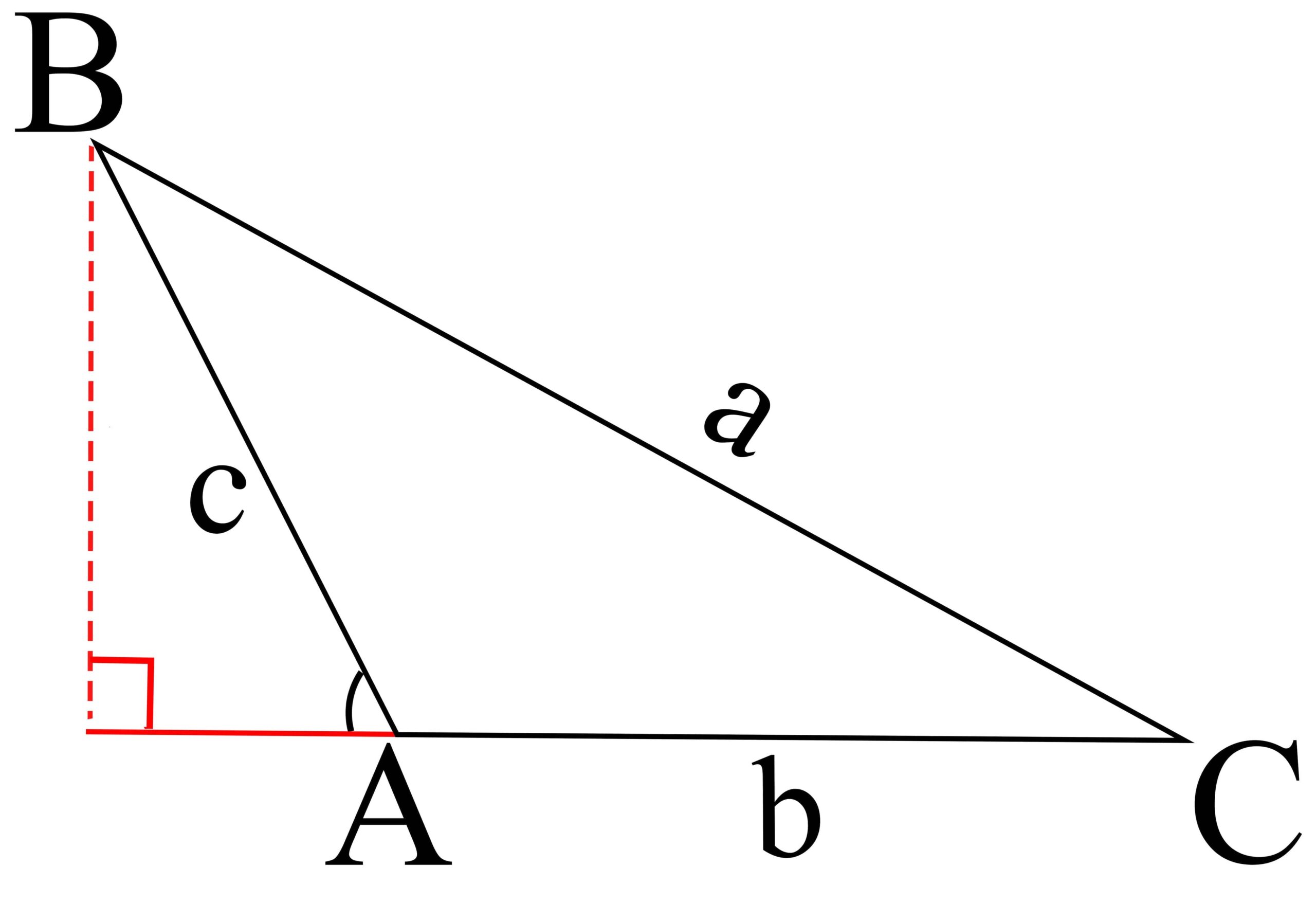
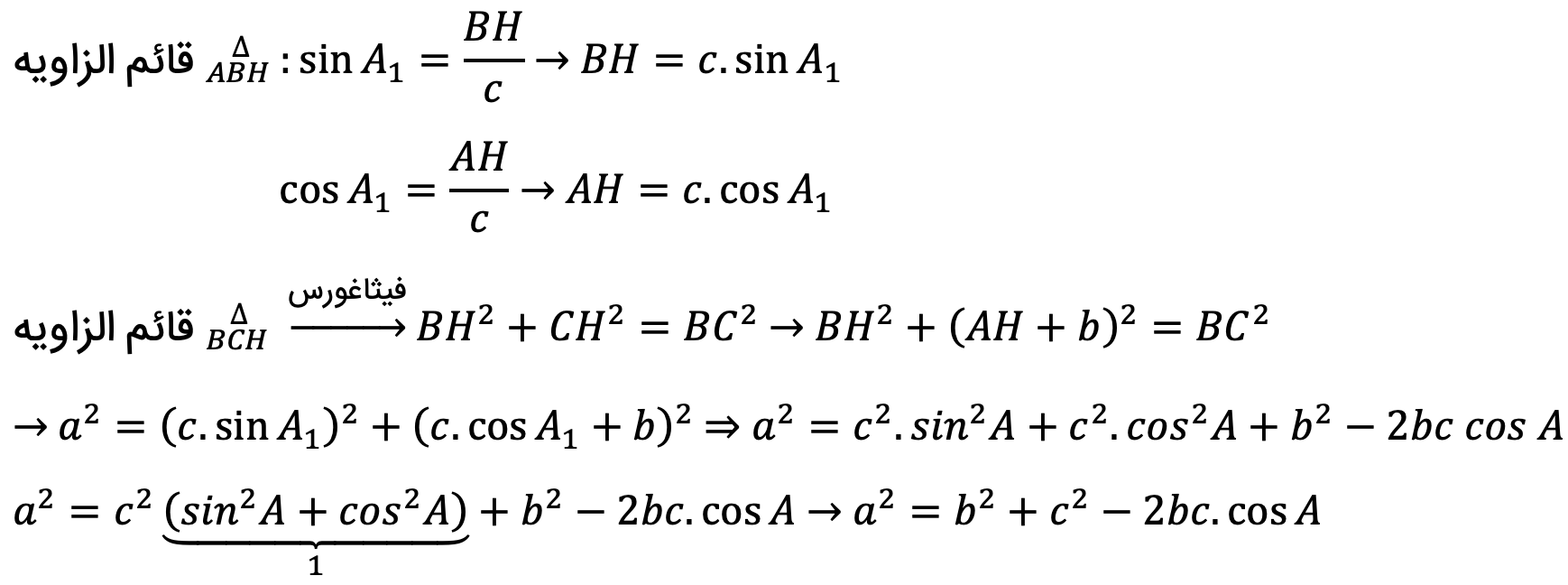
نیمساز ها در هندسه
در این بخش به قضیه نیمساز های زاویه های داخلی مثلث و محاسبه ی طول نیمساز ها خواهیم پرداخت.
قضیه نیمساز ها: در هر مثلث، نیمساز هر زاویه ی داخلی، ضلع روبرو به آن زاویه را به نسبت اندازه های ضلع های آن زاویه تقسیم می کنند.
اثبات) از رأس C خطی به موازات نیمساز AD رسم کرده سپس ضلع AB را مطابق شکل از رأس A امتداد می دهیم، تا دو خط همدیگر را در نقطه E قطع کنند:
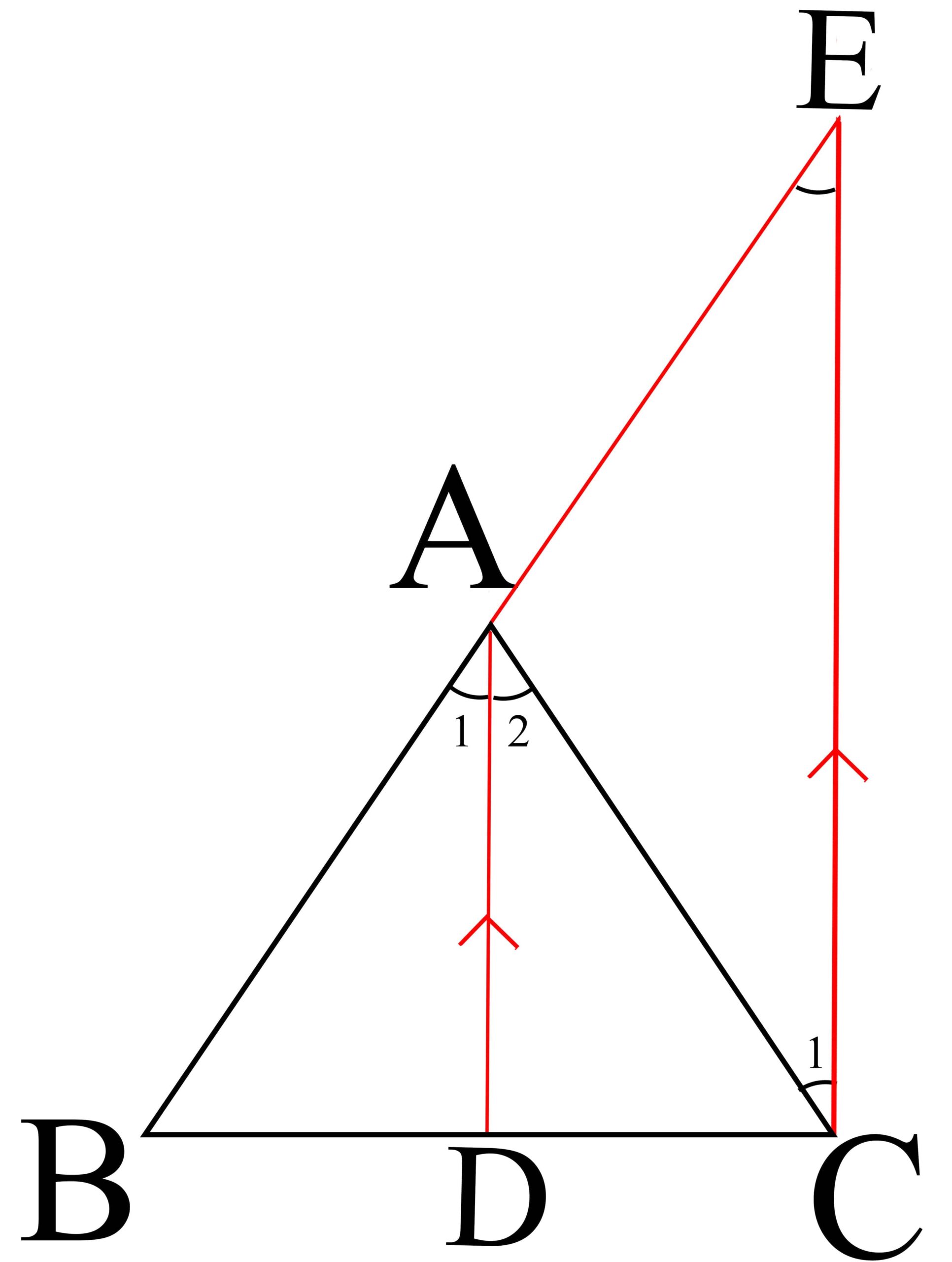
![]()
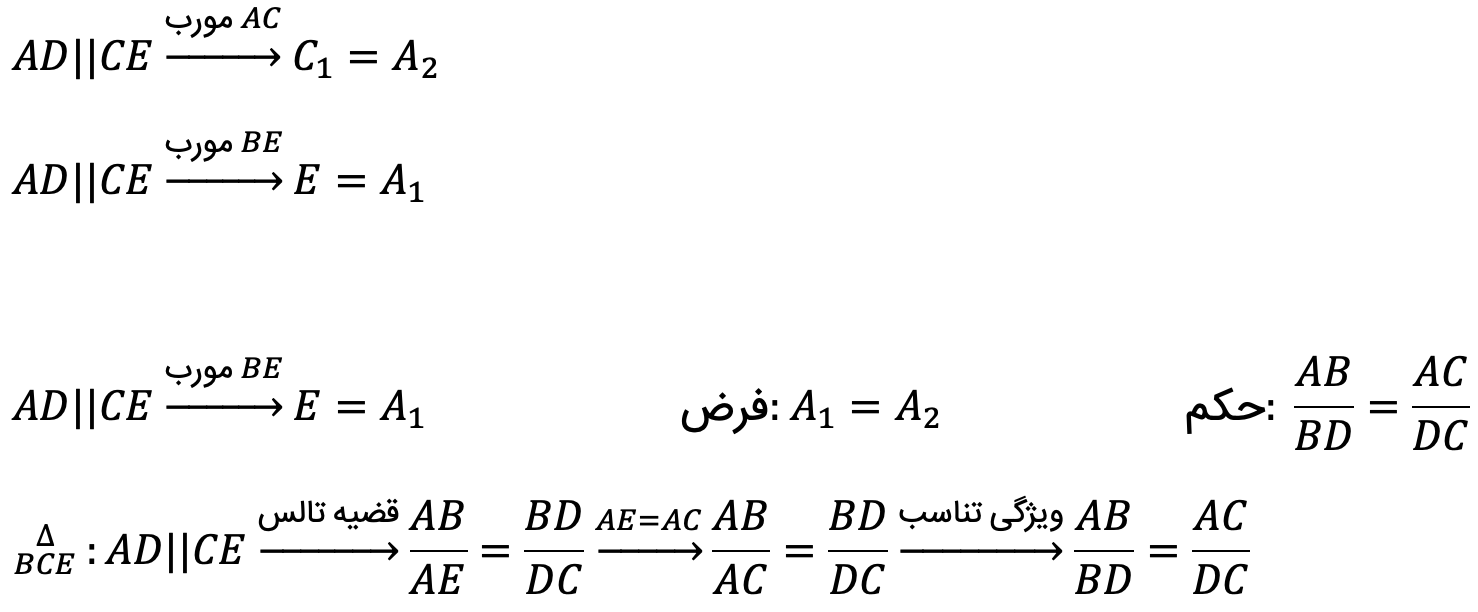
قضیه طول نیمساز مثلث: در هر مثلث، مربع اندازه ی هر نیمساز داخلی، برابر است:
زاویه ضلع ی اندازه ضرب حاصل-کند می ایجاد مقابل ضلع روی نیمساز که ای قطعه دو اندازه ضرب حاصل AD را امتداد می دهیم تا دایره را در E قطع کند، سپس E را به C وصل می کنیم:
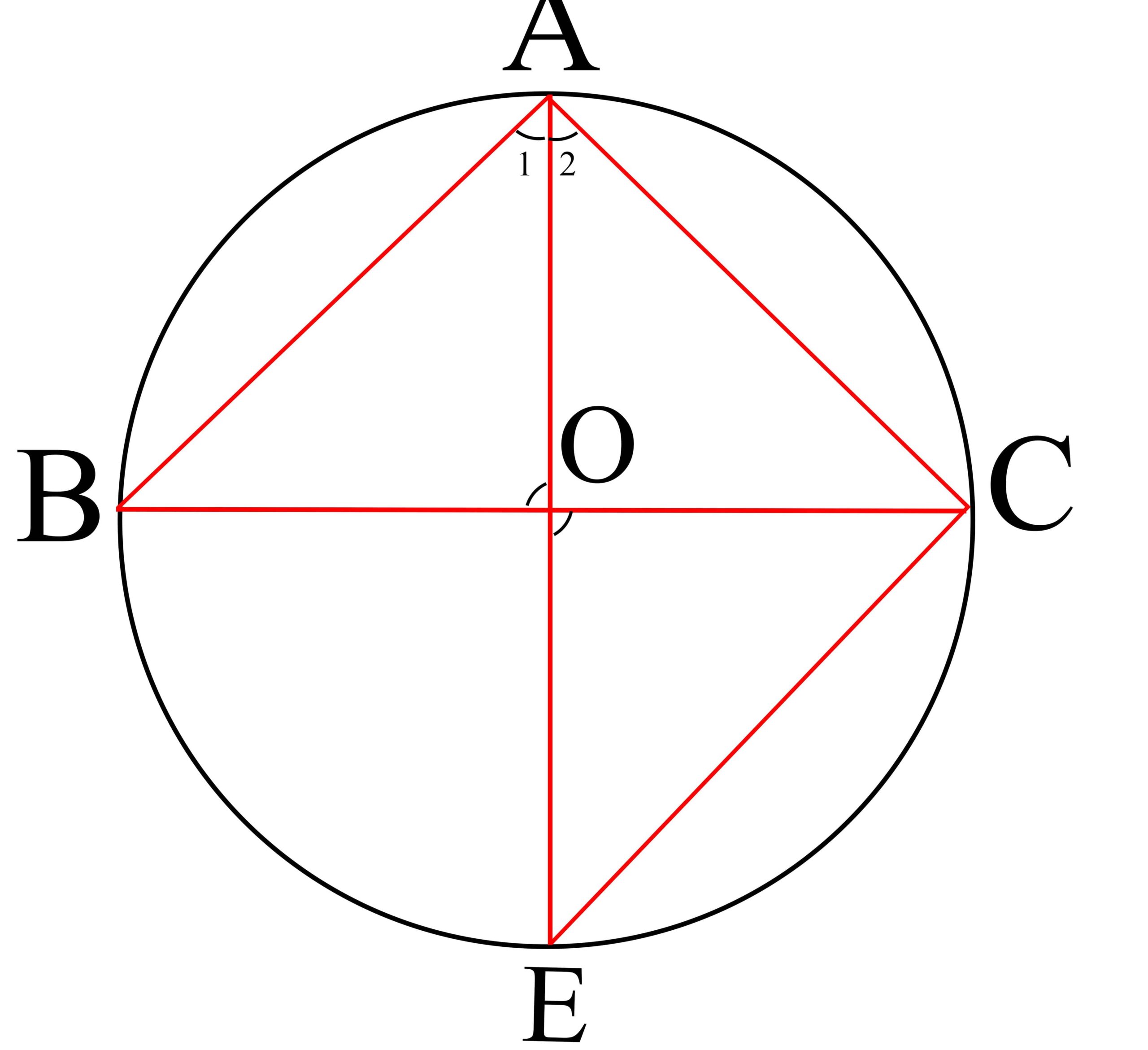
فرض: AD نیمساز
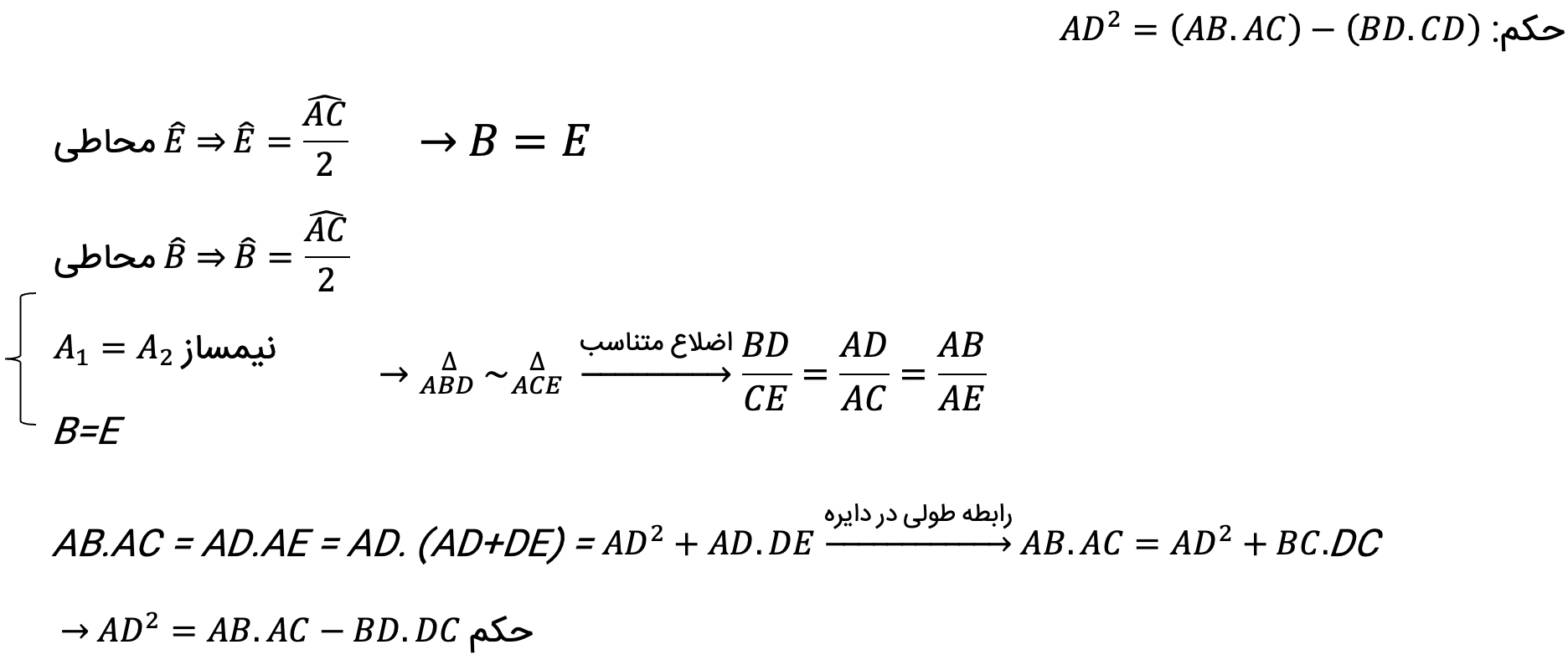
قضیه هرون در هندسه یازدهم
مثال) در مثلث ABC با اضلاع 13، 14 و 15، ارتفاع AH را رسم کنید.
مطابق شکل مقادیر x و y را بدست می آوریم و سپس مساحت مثلث ABC را محاسبه خواهیم کرد:
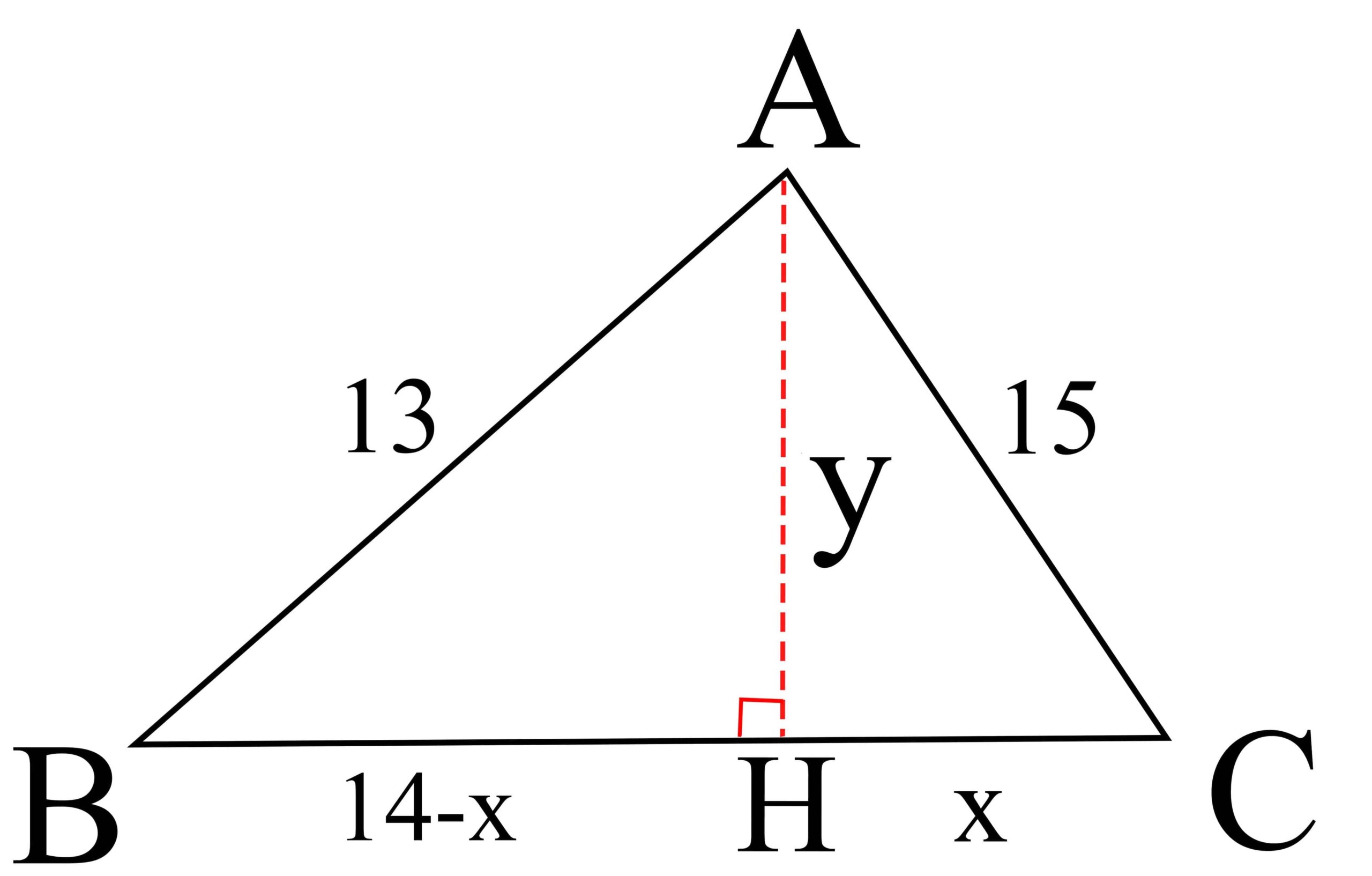
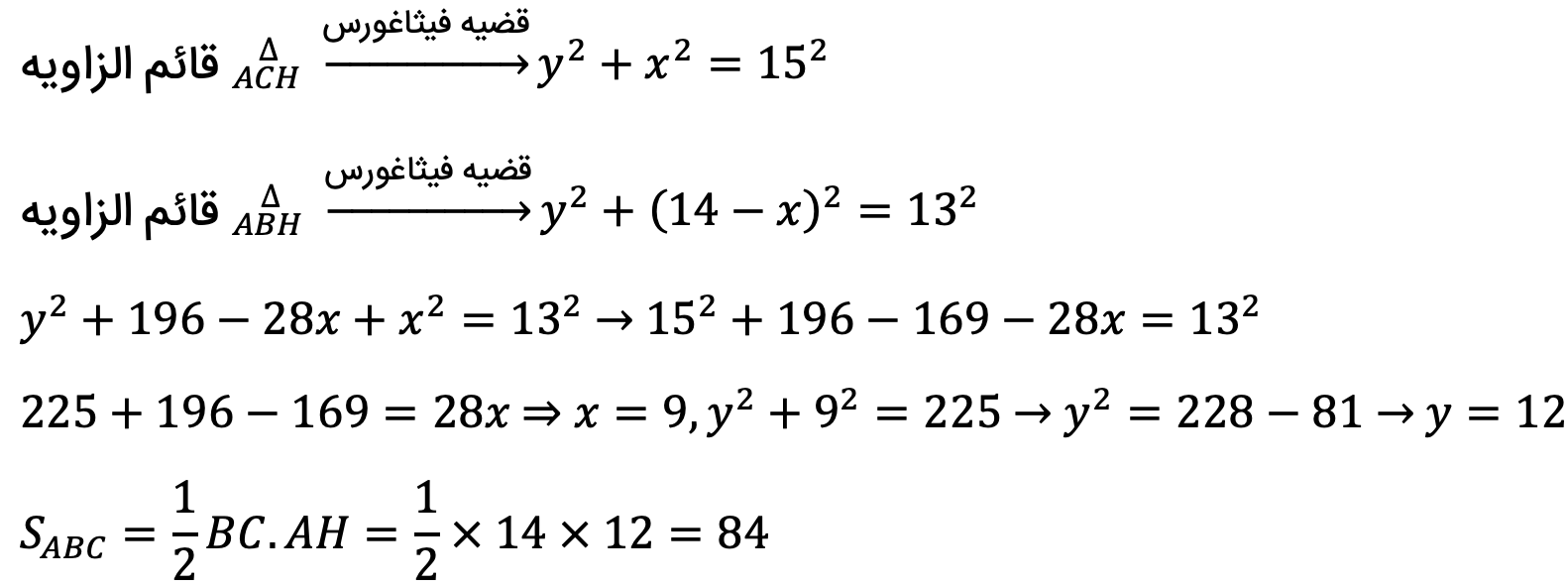
اگر همین روش مثال فوق را در حالت کلی در مثلث ABC که در آن BC=a، AC=b و AB=c به کار ببریم آنگاه، به قضیه ای به نام هرون می رسیم:
![]()
که در این رابطه P نصف محیط می باشد.
ارتفاع در مثلث
در مثلث ABC مطابق شکل داریم:
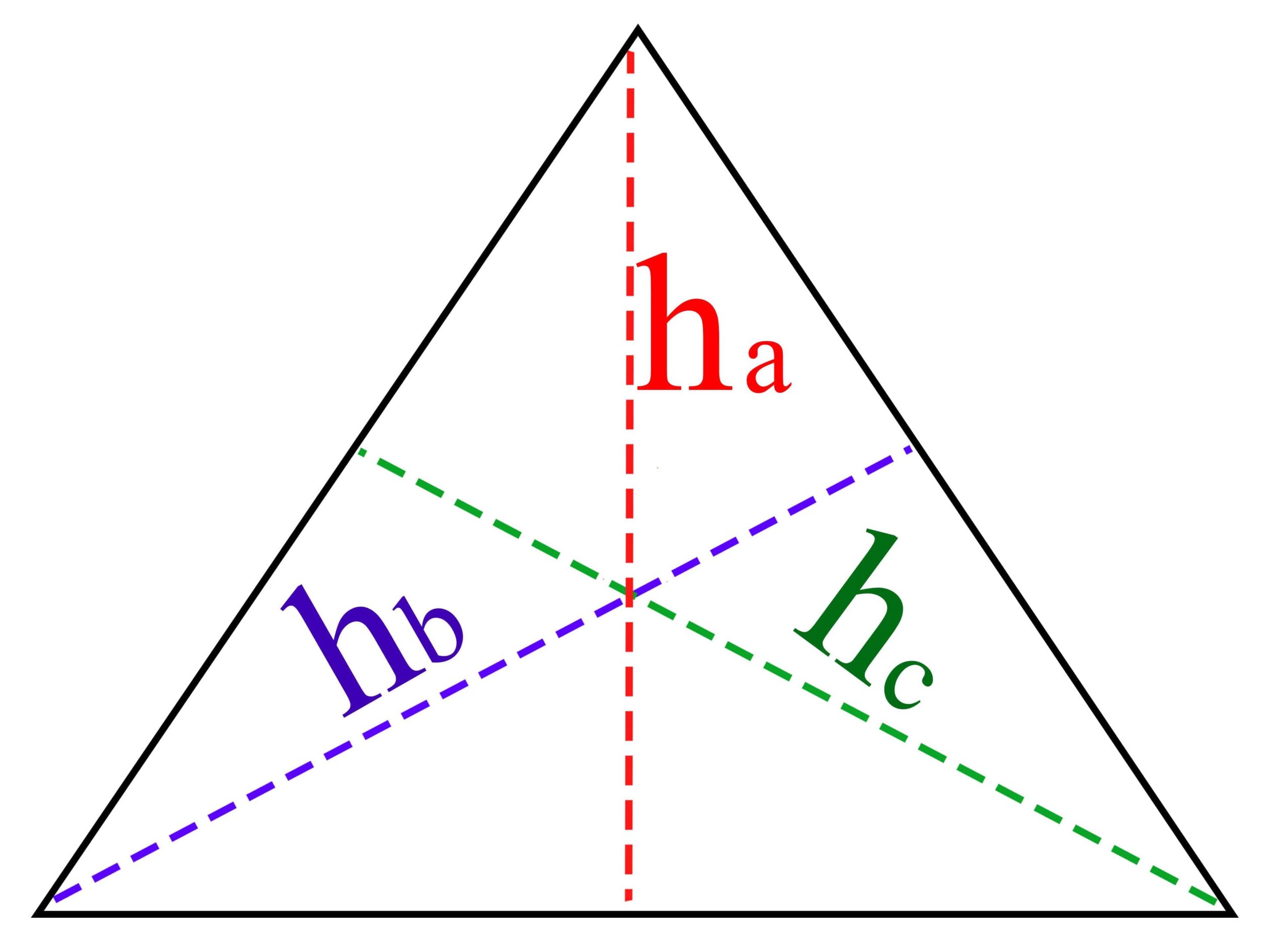
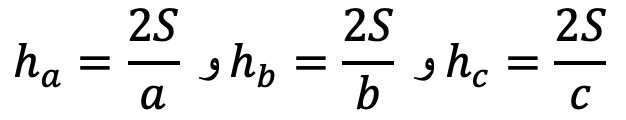
همچنین ببینید: حل تمرین هندسه یازدهم




