دوران و تقارن چرخشی در ریاضی
در مقاله دوران و تقارن چرخشی قصد داریم دومین بخش از فصل چهارم ریاضی را مورد بررسی قرار دهیم. در بخش اول از فصل چهارم با نحوه پیدا کردن قرینه یک شکل نسبت به نقطه یا خط آشنا شده اید. قبل از آشنایی با مباحث تازه به مرور بعضی از قسمت های پر اهمیت می پردازیم.

زاویه: ساده ترین تعریفی که می توان برای زاویه ارائه کرد این است که، به فضای گوشه ی بین دو خط که با یکدیگر برخورد کنند، زاویه می گویند. برای پیدا کردن زاویه نیز می توان از نقاله استفاده کرد، اما پیدا کردن بعضی از زوایا بسیار آسان است و دیگر نیاز به استفاده از نقاله نیست و به این زاویه ها، زاویه های اصلی می گوییم. هر کدام از این زاویه های اصلی را یک به یک روی شکل نشان می دهیم.
1) اگر دو خط موازی با یکدیگر برخورد کنند، زاویه ای که ایجاد می شود 180 درجه خواهد بود. زاویه 180 درجه به نیم دور نیز معروف است. به این معنی که هر شکل را که به اندازه نیم دور بچرخانیم، به زاویه 180 درجه می رسیم.
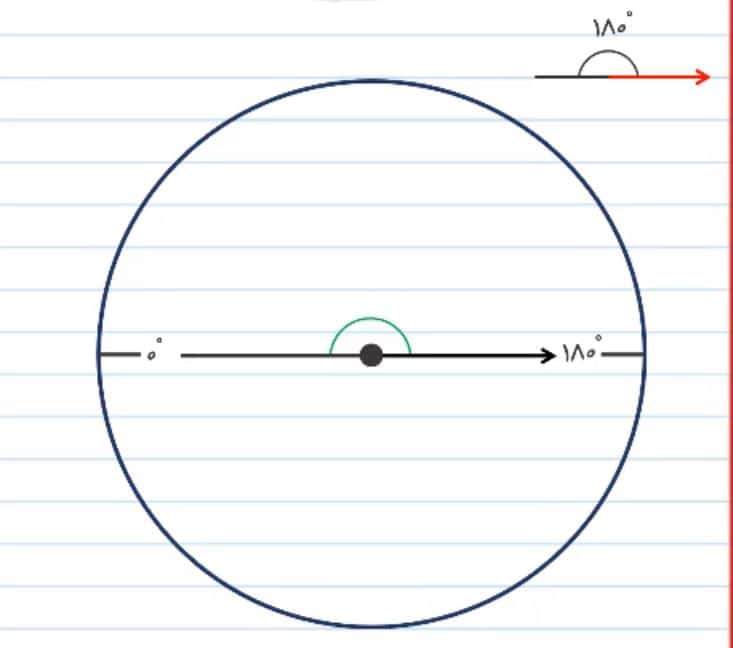
2) زاویه 90 درجه که نصف زاویه 180 درجه است و زاویه ای است که یکی از خطوط بر خط دیگر عمود شود. فضای گوشه بین این دو خط 90 درجه خواهد بود.
همچنین ببینید: آموزش دایره مثلثاتی
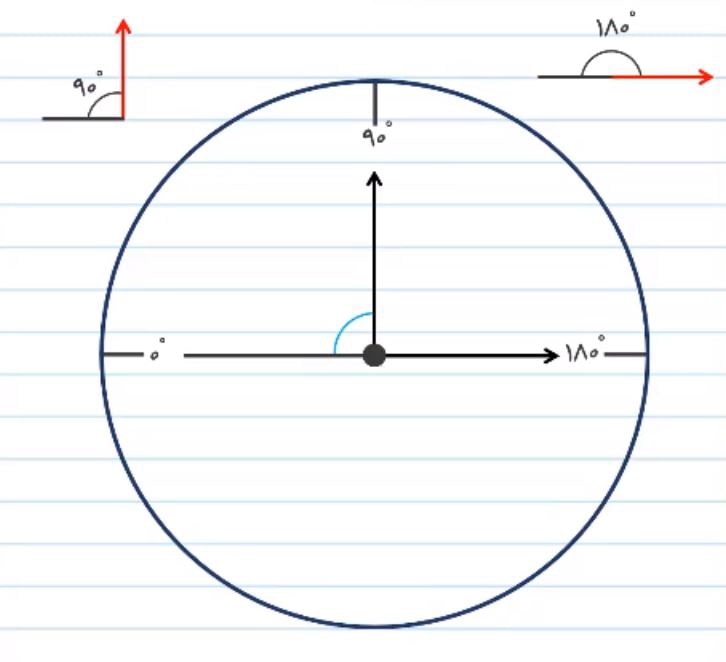
3) زاویه سوم، زاویه 270 درجه است که اگر پیدا کردن این زاویه برای شما دشوار است می توانید از زاویه های 180 و 90 درجه استفاده کنید. به این طریق که اگر زاویه 180 درجه و 90 درجه را با یکدیگر جمع کنیم به زاویه 270 درجه خواهید رسید.
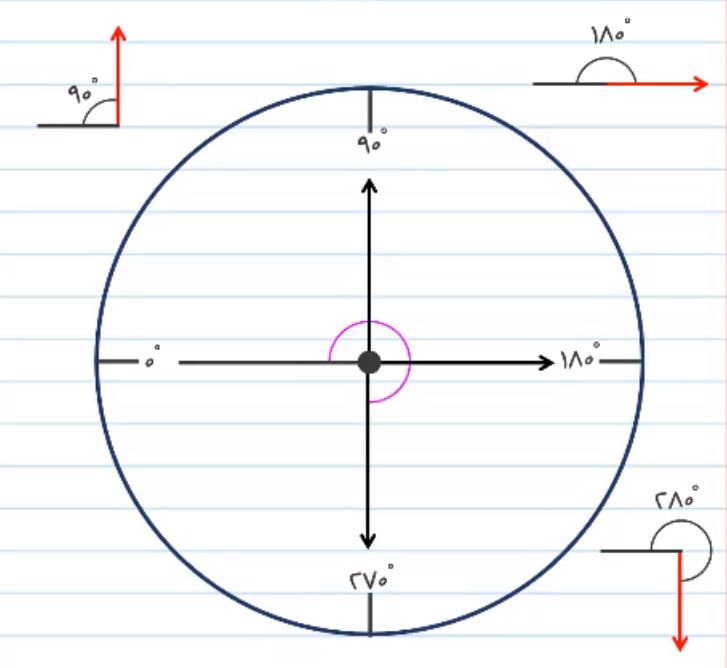
4) زاویه آخر 360 درجه است، یعنی یک دور کامل. به این منظور که اگر هر شکل را یک دور کامل بچرخانیم به زاویه 360 می رسیم. با توجه به شکل زیر مشخص می شود که زاویه های صفر درجه و 360 درجه در یک راستا قرار می گیرند.
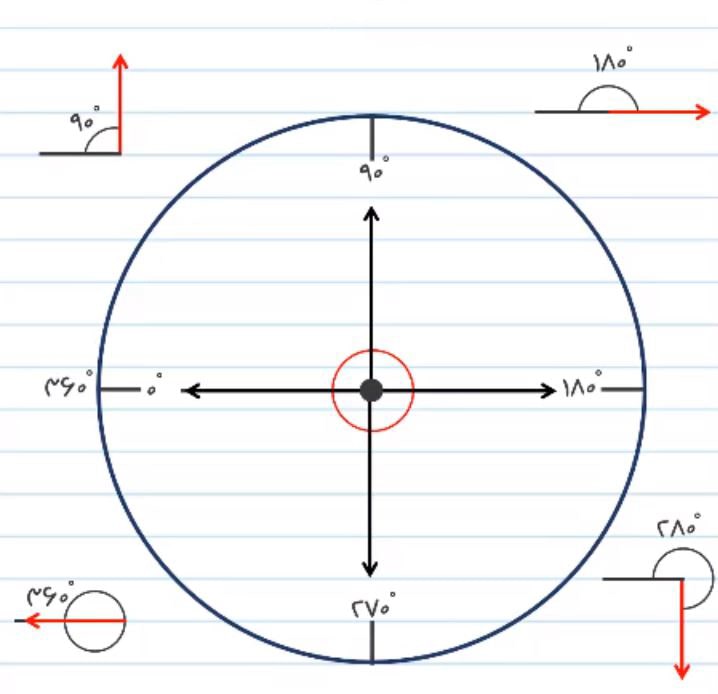
5) زاویه 45 درجه: یعنی اگر نیمساز زاویه 90 درجه را رسم کنیم، به زاویه ی 45 درجه خواهیم رسید.
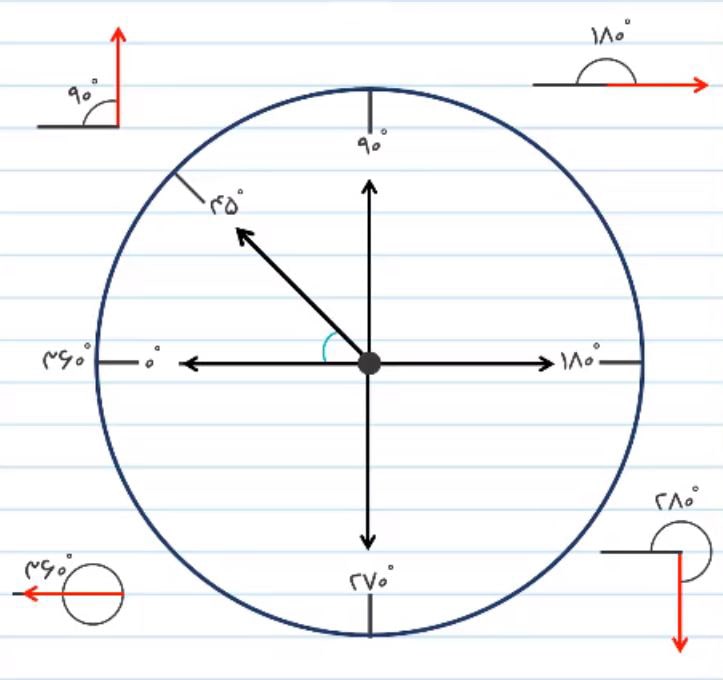
6) اگر زاویه 90 درجه را به 3 قسمت تقسیم کنیم هر کدام از زوایا، 30 درجه خواهند بود.
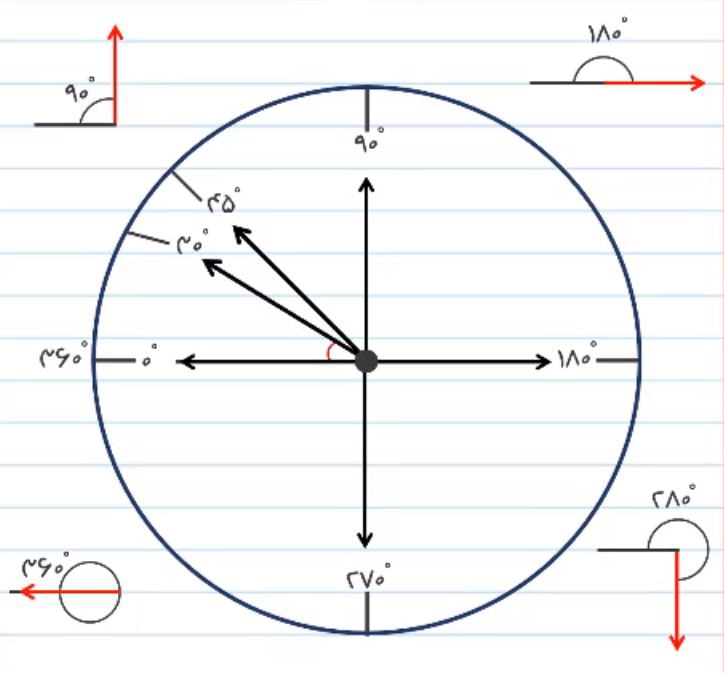
تقارن چرخشی اشکال هندسی
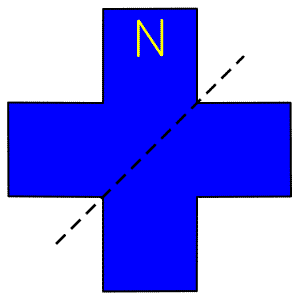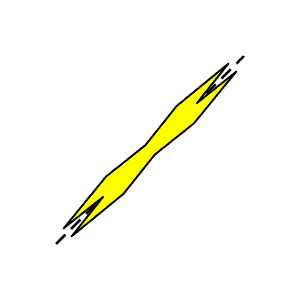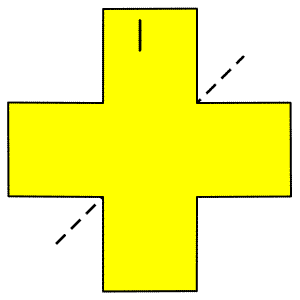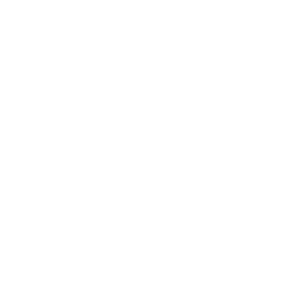
به چرخاندن اشیا و یا اشکال، دوران می گویند. به شکل زیر توجه کنید، می خوایم فلش را در زاویه های مختلف بچرخانیم:
ابتدا 90 درجه:
یکی از روش هایی که می توان برای چرخاندن این فلش استفاده کرد، طلق شفاف است. به این صورت که طلق شفاف را روی شکل و نقطه قرار می دهیم و سپس شکل و نقطه را روی طلق رسم می کنیم، در آخر به اندازه 90 درجه می چرخانیم.
چرخش 180 درجه:
شکل دقیقاً برعکس می شود:
در واقع چرخش به اندازه 180 درجه به عنوان قرینه شناخته می شود.
چرخش به اندازه 270 درجه:
یعنی یک چرخش 180 درجه و سپس یک چرخش 90 درجه:

360 درجه:
همانطور که گفته شد، پس از چرخش 360 درجه، شکل مجدداً روی خودش خواهد افتاد:
تقارن چرخشی
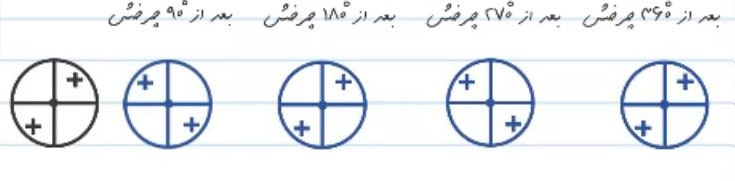
به چرخش شکل دوم توجه کنید:
همچنین آموزش جذاب آموزش لگاریتم را ببینید
همان طور که در شکل دوم می بینید، این شکل یک نوع دیگر چرخش را دارد که به آن تقارن چرخشی می گویند. در واقع تقارن چرخشی یعنی اینکه، وقتی شکلی را حول یک نقطه به اندازه ی 180 درجه یا کمتر می چرخانیم و شکل روی خودش می افتد، می گوییم شکل تقارن چرخشی دارد.
یادتان باشد که تقارن چرخشی با تقارن مرکزی بسیار به هم شباهت دارند اما یک تفاوت مهم دارند و آن هم این است که در تقارن مرکزی چرخش حتماً باید 180 درجه باشد اما در تقارن چرخشی، یا 180 درجه خواهد بود و یا کمتر از آن. یعنی اینکه اگر شکل را کمتر از 180 درجه هم بچرخانیم و مجدداً شکل روی خودش افتاد، شکل تقارن چرخشی خواهد داشت.
به یک مثال دیگر توجه کنید:
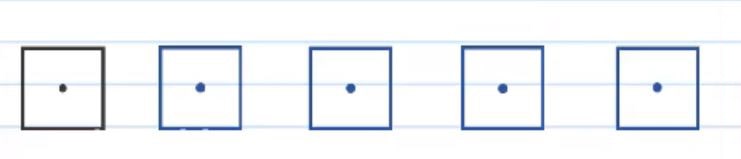
به دو شکل زیر توجه کنید، می خواهیم ببینیم دو شکل در چه زاویه ای با یکدیگر تقارن چرخشی دارند؟
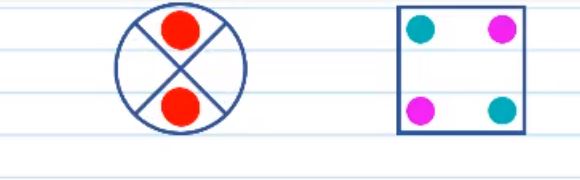
با استفاده از طلق شفاف، شکل را آنقدر می چرخانیم تا مجدداً روی خودش بیفتد. در شکل سمت چپ باید 180 درجه بچرخانیم تا این اتفاق بیفتد و چون در زاویه 180 این اتفاق رخ داده است پس می توانیم نتیجه بگیریم که شکل علاوه بر تقارن چرخشی، تقارن مرکزی نیز دارد. در شکل سمت راست نیز در 180 درجه این اتفاق رخ خواهد داد و می توان همان نتیجه گیری های شکل سمت چپ را برای شکل سمت راست نیز در نظر گرفت.
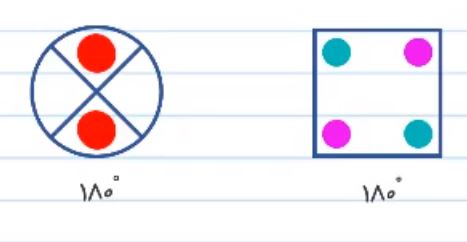
تقارن شکل های منتظم
بعضی از اشکال هستند که به راحتی و بدون چرخش، به راحتی متوجه می شویم که در چه زاویه ای تقارن چرخشی خواهند داشت. این اشکال، شکل های منتظم هستند. اشکال منتظم یعنی شکل هایی که زاویه ها و ضلع های متناظرشان با هم برابر باشد.
شکل مثلث:
همه زاویه ها و همه ضلع ها با هم برابرند. می خواهیم بدون استفاده از طلق شیشه ای متوجه شویم در چه زاویه ای تقارن چرخشی دارد. همان طور که یاد گرفتید یک دور کامل یعنی 360 درجه. در شکل مثلث ما 3 زاویه داریم، در نتیجه برای پیدا کردن تقارن چرخشی باید 360 را به 3 تقسیم کنیم که معادل با 120 درجه است. بنابراین نتیجه می گیریم که شکل زیر در زاویه 120 درجه تقارن خواهد داشت.
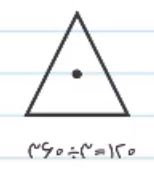
یادتان باشد مثلث فقط تقارن چرخشی دارد و تقارن مرکزی ندارد به این علت که اگر مثلث را به اندازه 180 درجه بچرخانیم، روی خودش قرار نمی گیرد.
شکل لوزی:
در شکل لوزی، تمام اضلاع و تمام زاویه ها با یکدیگر برابر هستند، پس یک دور کامل یعنی 360 درجه را به تعداد زاویه های لوزی تقسیم می کنیم، که در لوزی 4 زاویه داریم. لوزی در 90 درجه تقارن چرخشی دارد.
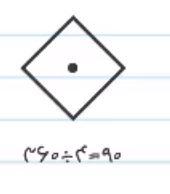
پنج ضلعی:
در پنج ضلعی نیز تمام ضلع ها و زاویه ها با یکدیگر برابر هستند. در پنج ضلعی 5 زاویه وجود دارد، در نتیجه در زاویه 72 درجه تقارن چرخشی خواهد داشت.
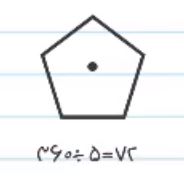
به شکل زیر توجه کنید. در این شکل نیز تمام اضلاع و زاویه ها با یکدیگر برابر هستند:
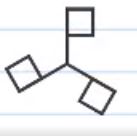
نقطه مرکزی شکل را مشخص می کنیم:
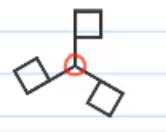
همانطور که مشاهده می کنید در نقطه مرکزی، سه زاویه داریم. در نتیجه این شکل نیز در زاویه 120 درجه تقارن چرخشی خواهد داشت.
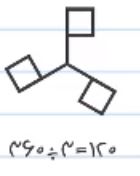
شش ضلعی:
این شکل نیز زاویه ها و اضلاع یکسانی دارد و با توجه به اینکه دارای 6 زاویه است در 60 درجه تقارن چرخشی خواهد داشت.
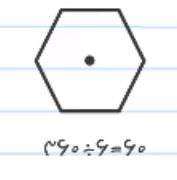
شش ضلعی تقارن مرکزی نیز دارد به این علت که اگر آن را 180 درجه بچرخانیم، در این زاویه روی خودش میفتد.











دیدگاهتان را بنویسید