دوران حول محور در هندسه

با مفهوم دوران از پایه های پایین تر از هفتم، هشتم و نهم نیز آشنا شده اید. اما دوران حول محور مربوط به رده های تحصیلی پایین تر با دوران مقاطع تحصیلی متوسطه اول یک سری تفاوت دارد. اگر یه یاد داشته باشید شما در دوران سال های قبل، یک مرکز دوران داشتید که اصطلاحاً به دوران مرکزی معروف بود و دارای دو عامل، مرکز دوران ¹ و زاویه دوران ² بود.

به عنوان مثال به شما گفته میشد یک پاره خط را حول یک نقطه خاص به اندازه زاویه ای معادل 90 درجه دوران بدهید. که آن نقطه مشخص به عنوان مرکز دوران شناخته میشد و برای انجام عملیات دوران از یک سر پاره خط به مرکز دوران اتصال می دادیم و یک زاویه 90 درجه ایجاد می کردیم. جهت زاویه نیز بایستی مشخص میشد که ساعتگرد بود و یا پاد ساعتگرد.

دوران حول محور

اگر پاره خط را AB نامگذاری کنیم و A را به O (مرکز دوران) متصل کرده باشیم، به اندازه طول OA روی پاره خط دومی که زاویه 90 درجه را روی آن شکل دادیم علامت می زدیم و آن نقطه A’ نامیده می شد. نقطه B نیز همانند A به O وصل میشد و مجدداً زاویه 90 درجه یا با نقاله و یا با گونیا ایجاد می کردیم  به اندازه طول BO روی ضلع دوم 90 درجه علامت می زدیم و نقطه B’ تشکیل داده میشد. که در واقع دو نقطه جدید ایجاد شده تصویر نقاط اصلی پاره خط AB هستند با دورانی معادل زاویه 90 درجه  و به عنوان مثال در جهت عقربه های ساعت، در نهایت کافی است که دو نقطه جدید را به هم وصل کنیم و پاره خط دوران یافته تشکیل داده می شود.

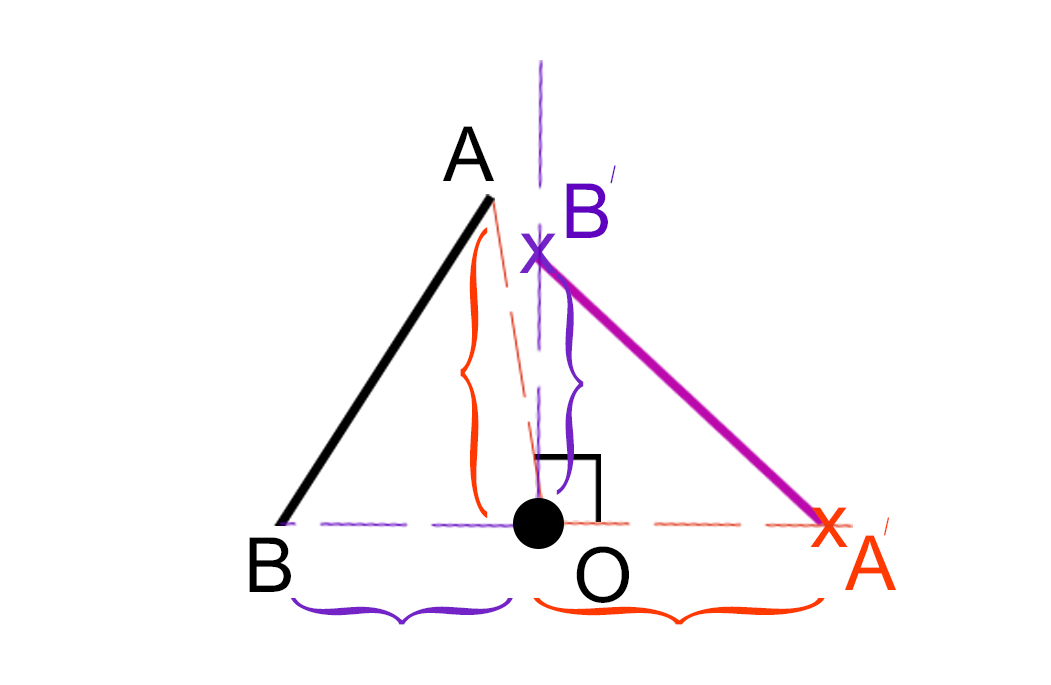
این نوع دوران را در پایه تحصیلی یازدهم، مطالب بیشتری را به خود اختصاص می دهد و همچنین دو نوع تبدیل هندسی دیگر نیز به آن اضافه می شود، یکی تقارن (بازتاب) و دیگری انتقال می باشد و در هندسه یازدهم مطالب کامل تر و مثال های متعدد تری را شامل می شود.

اما در این مطلب نوع دیگری از دوران را قصد داریم بررسی کنیم و آن دوران محوری است. خود مفهوم دوران به معنای چرخش است، چرخش حول یک محور و یا یک خط را دوران محوری می نامند.  به طوری که اگر یک پاره خط را حول پاره خطی دیگر چرخش دهیم تشکیل یک دایره می دهد. دایره ای که پاره خطی که آن را چرخانده ایم به عنوان شعاع دایره در نظر گرفته می شود.

در حالتی که اگر دایره ای را حول یکی از قطر های آن رسم کنیم، تشکیل یک کره می دهد. در نظر داشته باشید که قطر کره نیز همان قطر دایره خواهد بود. همچنین اگر نیم دایره ای را حول قطر دوران دهیم، باز هم تشکیل یک کره می دهد که قطر آن همان قطر نیم دایره خواهد بود. در نظر داشته باشید اگر همین نیم دایره را حول شعاع عمود بر قطر دوران دهیم، تشکیل نیم کره می دهد.

 و همینطور در خصوص ربع دایره ای که حول شعاع دوران داده می شود، باز هم نیم کره ای به مرکز و قطر ربع دایره تشکیل می دهد.

حالت های دیگر دوران حول محور

• اگر دو پاره خط موازی داشته باشیم و یکی از آنها را حول دیگری دوران دهیم، تشکیل استوانه خواهد داد. یه این دلیل که باید هر دو سر پاره خط را دوران دهید و اگر این دوران را در تک تک نقاط پاره خط انجام دهید به یک استوانه خواهید رسید، که البته استوانه ای تو خالی می باشد. به صورتی که شعاع قاعده استوانه، همان فاصله ی دو خط موازی خواهد بود.
• اگر مستطیل را حول یک محور بچرخانیم، باز هم همانند دو پاره خط موازی تشکیل استوانه خواهد داد با این تفاوت که آن استوانه تو پر خواهد بود. به صورتی که شعاع قاعده استوانه، عرض مستطیل خواهد بود.
• مستطیلی که در وسط آن یک محور تقارن برای آن در نظر گرفته شده است و حول آن مستطیل را می چرخانیم، باز هم استوانه ای تو پر ایجاد می شود.

کاربرد دوران حول محور

یکی از کاربرد های اساسی دوران حول محور، محاسبه حجم حاصل از دوران است. به بیان دیگر محاسبه حجم جسم دوار. برای درک بهتر این مطلب تابع y=f(x) را در نظر بگیرید که به صورت زیر باشد:

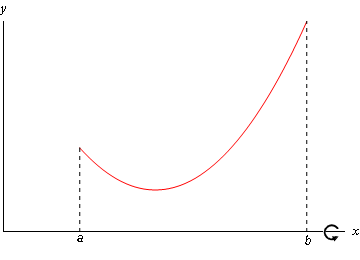
اکنون تصور کنید که این نمودار قرار است حول محور x دوران پیدا کند. در چنین حالتی، یک حجم سه بعدی بصورت زیر حاصل خواهد شد:

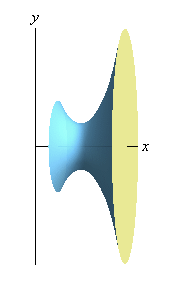
ما قصد داریم با استفاده از دوران ایجاد شده، حجم بدست آمده را محاسبه کنیم. به این صورت که حجم مورد نظر در هر مقطع، معادل حاصل ضرب مساحت سطح مقطع در آن نقطه، در ضخامت خواهد بود:

dV = A(x) dx

برای ادامه این محاسبات شما نیاز به تسلط روی مبحث انتگرال خواهید داشت و با انتگرال گیری می توانید حجم جسم دوار را محاسبه نمایید.

همچنین شاید مفید باشد: ترسیم های هندسی در ریاضی