توابع متناوب و خصوصیات آن

دانش آموزانی كه كنكوری هستند قطعا از اهميت فصل توابع برخوردار شده اند و قطعا با آن ها هم آشنا هستند، يكی از توابع بسيار مهم در دروس فيزيك هم از آن ذكر شده است، توابع متناوب و شبيه به توابع مثلثاتی می باشد. اين نوع از توابع ها و يا توابع مثلثاتی با زاويه های موج مطرح خواهند شد كه شيب های بسيار تندی را به همراه دارند؛ اين نوع مسائل در زندگی روزمره هم بسيار كاربرد دارد و قطعا در مثلثات رشته های رياضی و تجربی نيز اهميت خاصی برخورد دار است.
توابع متناوب:
برای پاسخ و تعريف به توابع متناوب بهتر است كه به تعريف رياضی آن بپردازيم، به صورت كامل اگر مقدار تابع در واحد های تكرار شونده و به صورت مدام حاصل گردد؛ به آن به اصطلاح توابع متناوب گفته می شود، شكل اين نوع از توابع را برخی از دانش آموزان با توابع سينويسی اشتباه می گيرند و آن ها را جزء نمودار های سينوسی محسوب می كنند، برای درك بهتر و توصيف اين نوع از توابع بايد عنوان شود كه مقدار شيب ها همانند موج های تند هستند و شما با در نظر داشتن اين موضوع ممكن نيست كه اشتباهی انجام دهيد.
توابعی كه تناوبی نباشند، توابع غير تناوبی هستند و مقدار تابع های متناوب را با P نمايش می دهند؛ اما در چه صورتی P متناوب و تابعی به آن نوع است؟ با كمی فكر كردن می توانيد پاسخ اين سوال را حدس بزنيد، در صورتی كه P مساوی با صفر قرار نگيرد و به صورت كلی می توان عنوان كرد كه x+p جزء پاسخ های دامنه اين نوع از توابع هستند.
يكی از نكات بسيار مهم كه بايد از آن غافل نشويد آن است كه مقدار تابع اصلی تناوب با مقدار p برابر خواهد بود.
يكی ديگر از خصوصيات بسيار مهم برای توابع متناوب؛ همگامسازی كردن آن با هندسه خواهد بود، تقارن های احتمالی بر روی آن به خوبی اعمال خواهند شد به صورتی كه اگر شما مقدار توابع متناوب را با متناظر رو به رو آن قرار دهيد می توانيد درك كنيد و به اين نتيجه برسيد كه الگو های يكسانی پديد خواهد آمد و قطعا اين موضوع امری عجيب نخواهد بود.( می توان شرح دادن كه مقدار الگو های منحنی بر روی يكديگر منطبق خواهند شد).
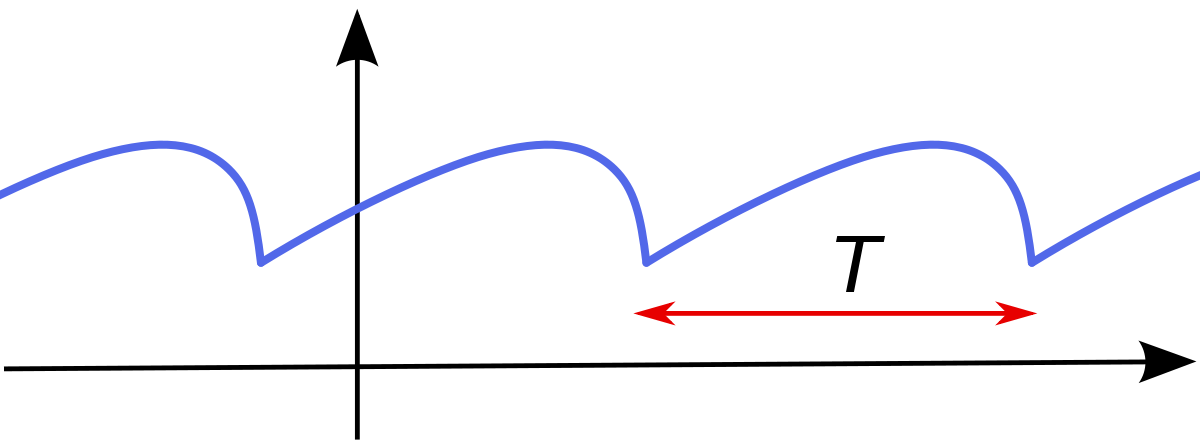
نكته: با تفاسير بخش قبلی می توانيد يك نتيجه بسيار مهم را دريافت كنيد، به صورت كلی توابع متناوب با فاصله متناوبش دارای تقارن است و قطعا با آن يكسان خواهد بود و قطعا كه دارای تقارن هستند.
انواع توابع متناوب:
انواعی از توابع های متناوب برای شما در اين بخش نام خواهيم برد، توجه داشته باشيد كه ممكن است برخی از آن ها را قبلا شنيده باشيد و البته در سال های قبلی با آن ها اشنا شده باشيد.
- توابع سينوسی: اولين تابع متناوبی كه برای شما شرح خواهيم داد تابع های سينوسی هستند، اين نوع از توابع ها شكلی همانند تپه هایی دارند كه با اين نام می توانيد آن ها را در ذهن خود به ياد بسپاريد، اين نوع از توابع ها مثلثاتی هستند. X + 2 π يكی از فرمول ها برای سينوس هستند.
- كسينوس ها: علاوه بر توابع سينوسی؛ كسينوس ها هم دركنار آن ها خواهند درخشيد. البته بهتر است بدانيد كه بر عكس سينوس ها در نمودار ها كشيده خواهند شد و البته كه اين نوع از توابع ها از مقدار y 1 شروع خواهد شد و بر خلاف سينوس ها كه از 0 شروع می شوند. دارای تناوب 2π هستند.( براساس توابع مثلثاتی است و مشخص میکند که بیان هر تابع تناوبی به کمک مجموع چندین تابع سینوسی یا توابع مثلثاتی دیگر میسر است)
- تابع جزء اعشاری: يكی ديگر از توابع تناوبی قطعا توابع های جزء اعشاری و يا تناوب هستند، نام ديگر آن ها نيز جزء صحيح می باشد. نماد آن را به اصطلاح به شكل px نمايش خواهند داد؛ بهتر است بدانيد كه روش حل مسائل جز صحيح بسيار آسان است به صورتی كه بايد به هر عدد داخل براكت يا جزء صحيح اعداد نزديك به آن ها را انتخاب كنيد.( يكی از سوالات بسيار مهمی كه طراحان سوال كنكور شما را با آن آزمايش می كند در رابطه با دامنه ها با جزء صحيح می باشد، شما بايد ابتدا جزء صحيح را محاسبه كرده و سپس تست را حل كنيد، شما بايد مقدار مساوی بودن اعداد را هم دقت كنيد)
خواص و ويژگی های تابع های متناوب:
داشتن مقدار های مناسب و عالی برای ويژگی های خواص متناوب در مقادير آن نهفته است؛ اما مقدار آن ها نيز در واحد های تكراری قرار داده شده است؛ اما در صورتی كه مقادير تابع اول با تابع دوم برقرار باشد، ولی بايد مقدار n در آن ها عدد صحيح باشد. داشتن مقادير حقيقی و صحيح برای حل سوالات تابع متناوب بسيار مهم هستند و قطعا كه بايد با آن ها قدم هایی را پيش بگيرد.
جمع بندی:
شما در اين مقاله به صورت تخصصی با موضوعات توابع متناوب آشنا شده ايد و اطلاعات كلی و جامع و خلاصه ایی را از آن ها دريافت كرديد؛ ما در انتهای اين مقاله چند نكته بسيار مهم را برای شما شرح خواهيم داد.
اولين نكته مهم در رابطه با نوع توابع متناوب است، شما بايد تمامی انواع آن ها را بشناسيد و البته روابط آن ها را هم به خاطر بسپاريد، سينوس و كسينوس و جزء صحيح و… اما شما می توانيد با دريافت كلی از ويژگی تمام آن ها،جمع بندی های ديگر را برای انواع ديگر داشته باشيد.
همچنین ببینید: معادله سیاله











دیدگاهتان را بنویسید