توابع جز صحیح به زبان ساده + فیلم آموزشی

تابع جز صحیح موضوع اصلی این پست است که توابع جز صحیح به زبان کاملا ساده میبندیم

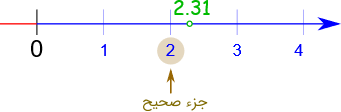
برای درک دقیق مفهوم جزء صحیح به جمله های زیر دقت کنید:

• جزء صحیح عدد 2.35، عدد 2 می باشد
• جزء صحیح عدد 4.36-، عدد 5- می باشد
• جزء صحیح عدد 1-، عدد 1- می باشد

همان طور که مشاهده می کنید، وجه اشتراک هر سه عدد بالا، این است که برای نوشتن جزء صحیح یک عدد، نزدیک ترین عدد صحیح کوچکتر یا مساوی آن را در نظر میگیریم. به بیان دیگر، عبارت جزء صحیح یک عدد، نزدیک ترین عدد صحیح کوچک تر یا مساوی با آن عدد است.

برای درک بهتر مطلب به جدول زیر توجه کنید.

عدد	جزء صحیح
1.1 –	2-
0	0
1.01	1
2.9	2
3	3

برای نمایش جزء صحیح یا تابع جزء صحیح از براکت استفاده می شود:

جزء صحیح x

جالب است بدانید  که تا دهه 1970 برای نمایش جزء صحیح از براکت کامل ( [ ] ) استفاده میشد و از آن به بعد از براکت ناقص  ( ⌊ ⌋ ) استفاده شد. البته هنوز هم به منظور نشان دادن تابع جزء صحیح، از براکت کامل استفاده می شود.

( در صورتی که در مبحث تقسیم چند جمله ای نیز مشکل دارید بر روی لینک روبرو کلیک نمایید.)

تعریف تابع جزء صحیح

همان گونه که در ابتدا با مفهوم جزء صحیح آشنا شدیم، تابع جزء صحیح را نیز با توجه به آن تعریف می کنیم. به این صورت که تابع جزء صحیح x را به طور معمول به صورت y=[x] نشان می دهند که به تابع براکت نیز معروف است. اما به زبان ریاضی تابع جزء صحیح دارای 3 تعریف می باشد:

با این فرض که x یک عدد حقیقی است، در این صورت:

تعریف 1: جز صحیح متغیر x، سوپریمم مجموعه اعداد صحیحی است که از x بزرگ تر نیستند:

[x]=sup{m∈Z: m≤x}

تعریف 2: جز صحیح عدد حقیقی x، بزرگ ترین عضو مجموعه اعداد صحیح زیر خواهد بود:

{m∈Z: m≤x}

تعریف 3: جز صحیح x، عدد صحیح منحصر به فرد  می باشد که در رابطه زیر صدق خواهد کرد:

[x]≤x<[x]+1

خواص تابع جز صحیح

با توجه به سه تعریف بالا، قصد داریم برخی از مهم ترین خواص تابع جز صحیح را بررسی کنیم.

[x]=a را در نظر بگیرید و a نیز عددی صحیح می باشد. بنابراین خواهیم داشت:

معادلات توابع جز صحیح

با توجه به تعاریف و خواص بیان شده، به راحتی می توان معادلات شامل توابع جز صحیح را به جواب رساند. برای درک بهتر به مثال زیر توجه کنید.

را حل کنید  [0.5+[x]]=20 مثال) معادله

برای حل این مثال، ابتدا فرض میگیریم که مقدار [X] برابر با مقداری مثل y  است و سپس y را در معادله داده شده جایگذاری می کنیم:

[0.5+y]=20

با توجه به تعریف تابع جز صحیح، رابطه بالا را می توانیم به نامساوی زیر تبدیل کنیم:

20≤y+0.5<21

اگر 0.5 را از طرفین کم کنیم به نامساوی زیر خواهیم رسید:

19.5≤y<20.5

بنابر فرض ابتدایی y را برابر با جز صحیح x گرفتیم، در نتیجه:

y=20=[x]

بنابراین مقدار x بصورت زیر خواهد بود

20≤x<21

نمودار تابع جز صحیح

با راحت ترین و ساده ترین تابع جز صحیح، یعنی y=[x] شروع می کنیم. همان طور که از ظاهر تابع مشخص است، نمودار آن نیز بصورت بازه ای خواهد بود و جدول زیر به خوبی بیانگر این مسئله است:

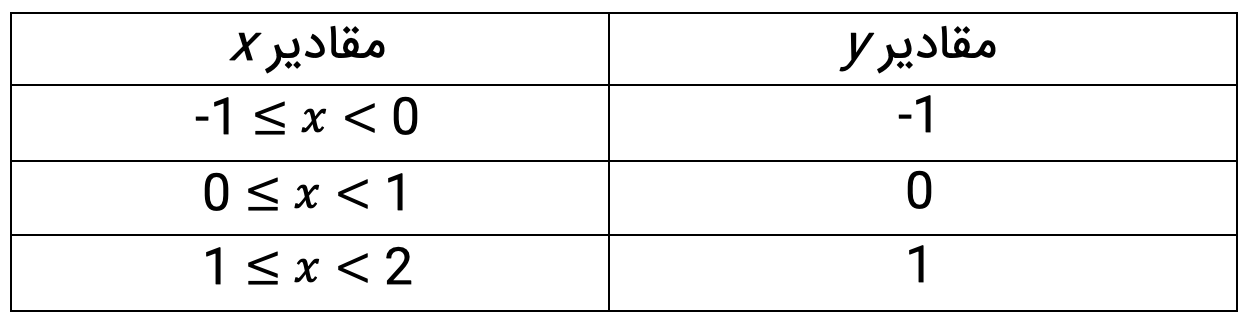
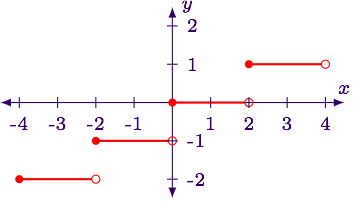
در نتیجه با توجه به جدول بالا نمودار تابع بصورت زیر خواهد بود:

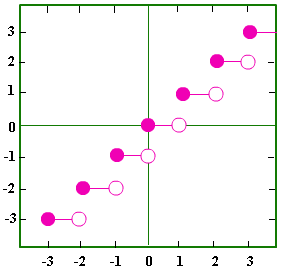
همان طور که می بینید با توجه به ظاهر خاص نمودار تابع جز صحیح، آن را پلکانی یا پله ای می نامند.

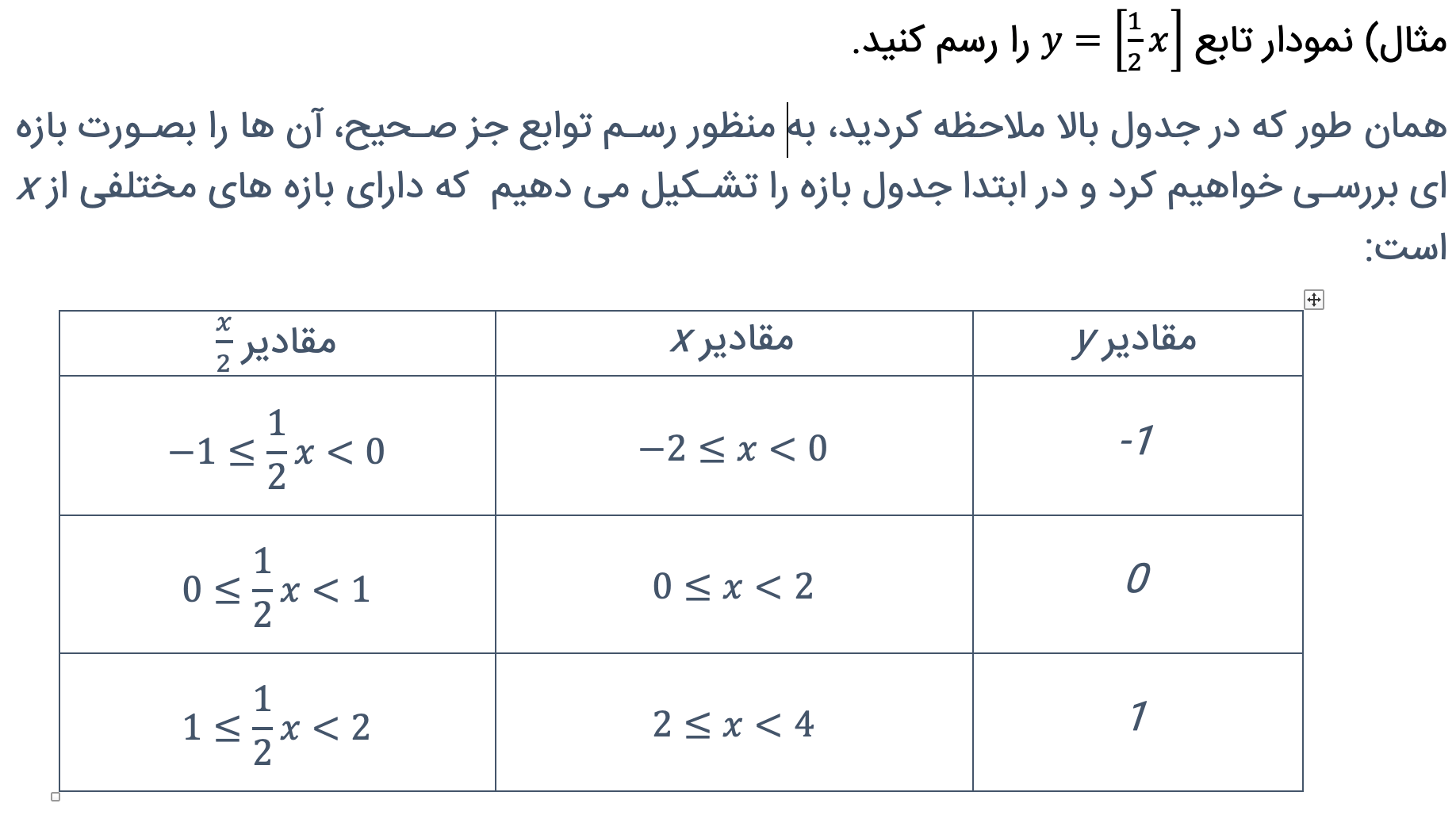
با در نظر گرفتن جدول بالا و همچنین با توجه به سه بازه در نظر گرفته شده، نمودار تابع داده شده بصورت زیر خواهد بود:

همچنین ببینید: آموزش ترسیم های هندسی