آموزش ترسیم های هندسی در ریاضی
مبحث ترسیم های هندسی هم در کتاب هندسه (1) پایه تحصیلی دهم و هم در کتاب پایه یازدهم رشته علوم تجربی به آن پرداخته می شود. برای درک بهتر بخش ترسیم های هندسی باید در ابتدا با مفهوم مکان هندسی آشنا شویم.
به بیان ساده، فرض کنید، مورچه ای داریم که آن را در جوهر میگذاریم و بعد از آن مورچه را روی کاغذ سفید رها می کنیم. مسیری که مورچه پس از حرکت روی کاغذ ایجاد می کند را مکان هندسی می گوییم. در واقع به فاصله ایجاد شده از نقطه خاص مکان هندسی گفته می شود.
در این مبحث، با دو مکان هندسی بسیار مهم سر و کار خواهیم داشت. یادتان باشد که در سؤالات باید شکارچی بسیار ماهری باشید، به این صورت که اگر در سؤال گفته شد، فاصله از یک نقطه مقدار ثابتی داشته باشد، یعنی اینکه باید یک دایره را رسم کنید. به این صورت که نقطه به عنوان مرکز دایره در نظر گرفته می شود و فاصله داده شده نیز به عنوان شعاع دایره خواهد بود.
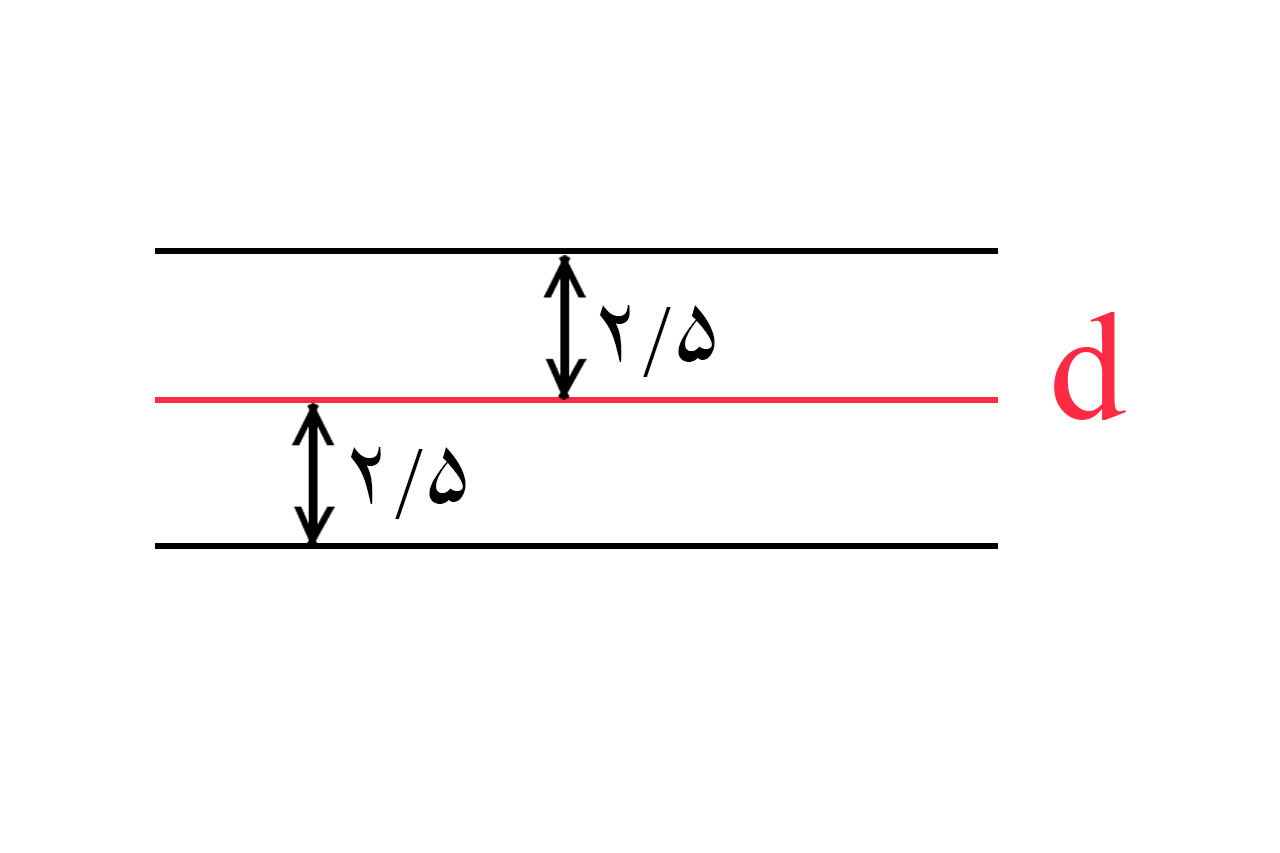
اما اگر در صورت سؤال گفته شد، فاصله از یک خط، می خواهد مقداری ثابت داشت باشد، دو خط موازی با آن خط مربوطه خواهد بود. به عنوان مثال اگر خطی به نام d داشته باشیم، اگر بخواهیم مکان هندسی نقاطی را روی آن پیدا کنیم که به اندازه 5/2 واحد از خط d فاصله داشته باشند، دو خط موازی با d باید ترسیم شود که فاصله شان با خط به اندازه 5/2 واحد باشد.
فیلم آموزشی ترسیم های هندسی
تاریخچه ترسیم های هندسی
انسان از همان ابتدا، از هندسه زیاد استفاده می کرده است به خصوص از ترسیم های هندسی. مثلاً فرض کنید یک کشاورز می خواهد زمین خود را به دو قسمت مساوی تقسیم کنید و فقط با رسم یک خط می تواند این کار را انجام دهد.
ترسیم های هندسی دهم
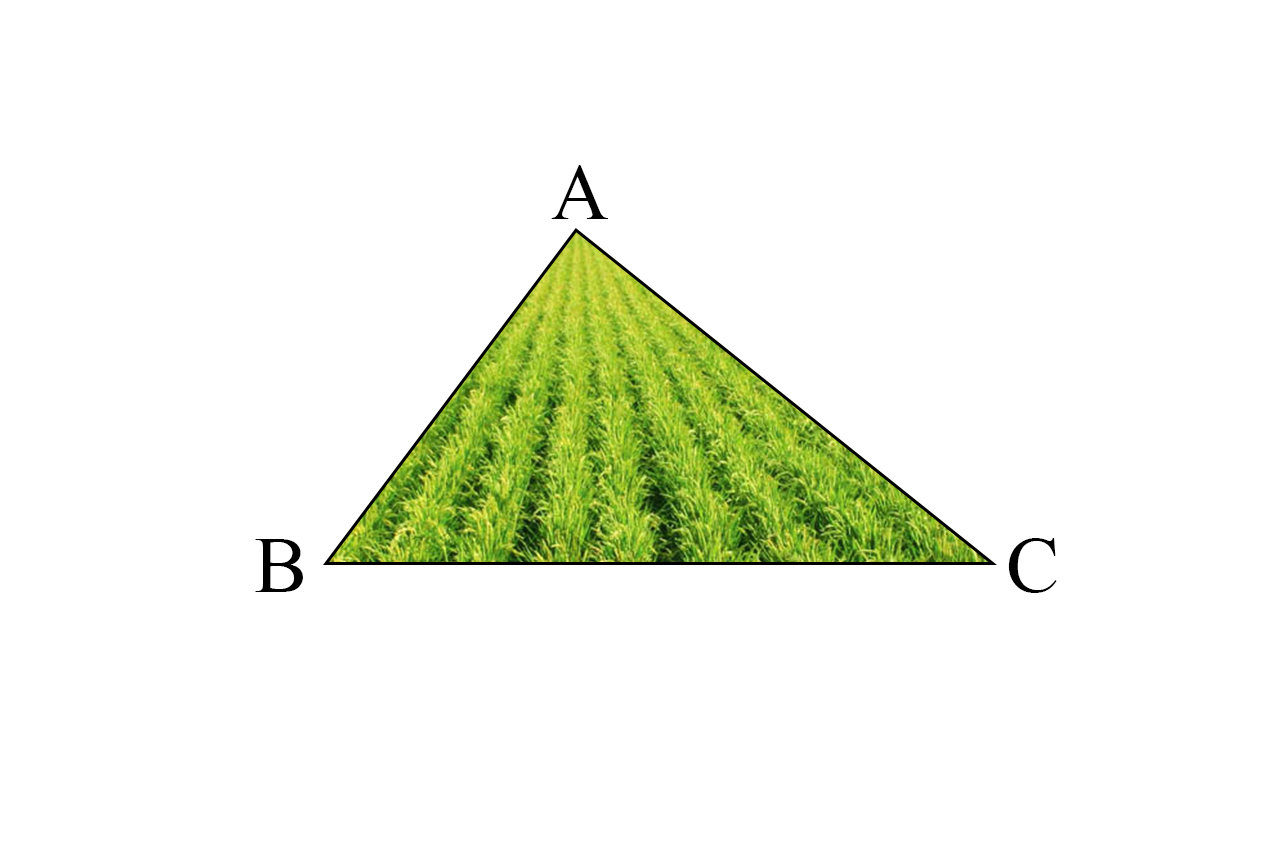
حال می خواهیم ببینیم به چه صورت این کشاورز می تواند زمین خود را تقسیم کند. فرض کنید زمین کشاورز مثلثی شکل است و اسم آن را ABC می گذاریم:
اگر وسط یکی از اضلاع را پیدا کنیم، و اسم آن را M بگذاریم و نقطه A به M را متصل کنیم، در واقع میانه یک ضلع را ترسیم کنیم، دو مثلث تشکیل خواهد شد و با دو مساحت S1 و S2 که فرض ما بر این است که هر دو مساحت با یکدیگر برابر هستند.
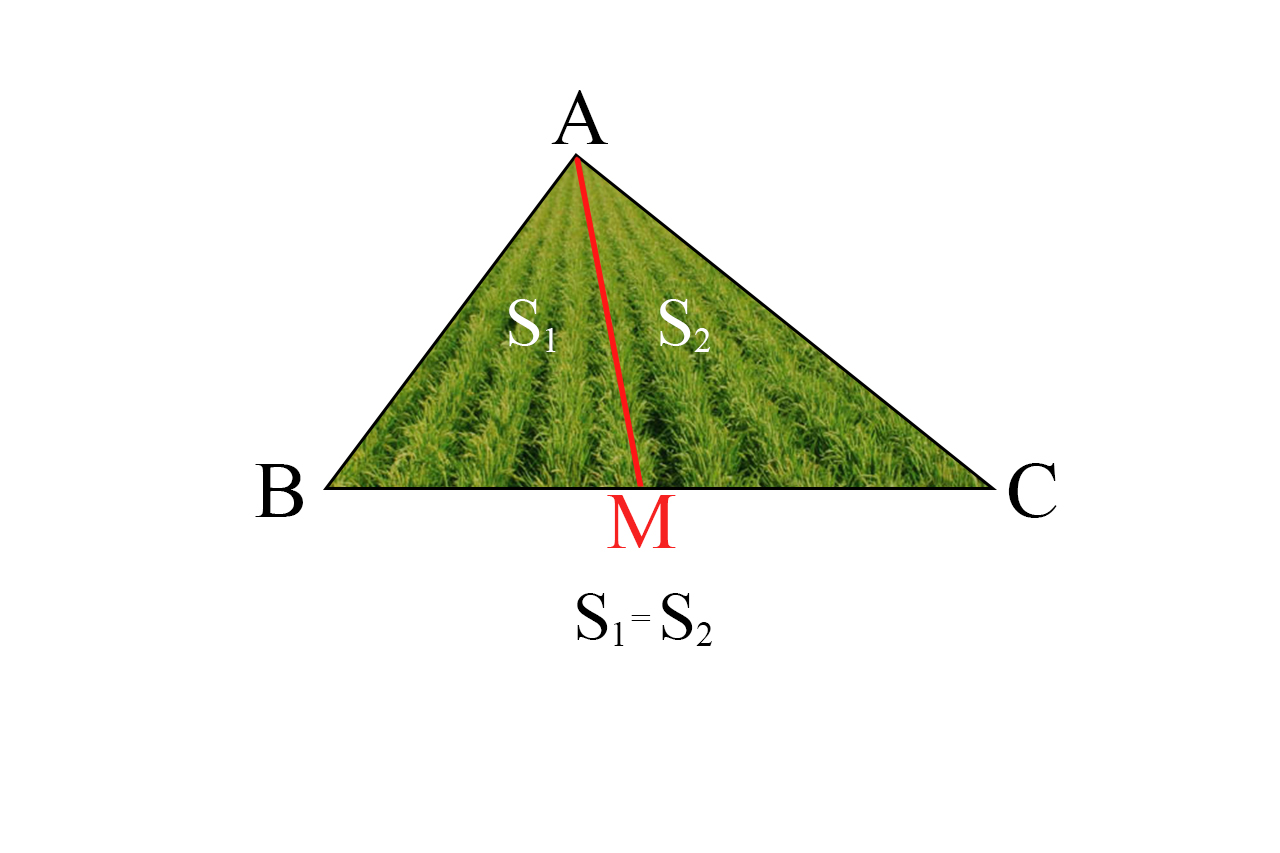
به این دلیل مساحت هر دو مثلث را برابر می دانیم که با استفاده از تعریف مساحت مثلث دو طرف تساوی با یکدیگر برابر خواهند بود:

همانطور که مشاهده می کنید هر دو مساحت پارامتر های یکسانی دارند ( یک دوم و ارتفاع AH)، مقادیر BM و CM نیز با یکدیگر برابر هستند ب این دلیل که نقطه M دقیقاً در وسط ضلع BC قرار گرفته است.
نکته: اگر یک نقطه در صفحه داشته باشیم، تمام نقاطی که فاصله آنها از این نقطه یکسان است، تشکیل دایره مثلثاتی خواهند داد. در واقع هر نقطه که از مرکز دایره به فاصله ی r باشد، روی دایره قرار دارد. در نتیجه هر نقطه ای که روی دایره قرار داشته باشد به فاصله r از نقطه O خواهد بود.
وضعیت دو دایره
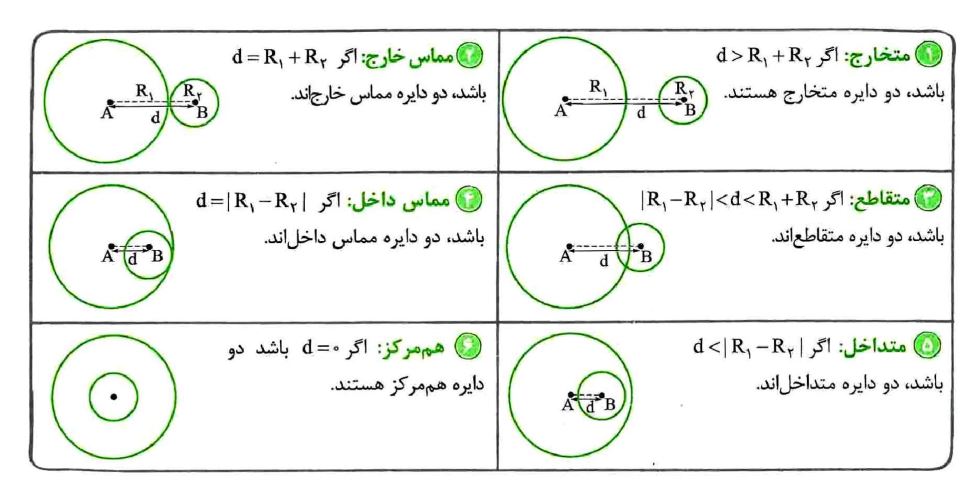
دو دایره نسبت به هم 6 وضعیت عمده دارند که برای دانستن وضعیت آنها باید فاصله مرکز ها (طول خط المرکزی) را بدانیم که آن را با d=AB نشان می دهیم و حال باید d را با R1+R2 و R1-R2 مقایسه کنیم که در این صورت 6 وضعیت پیش می آید.
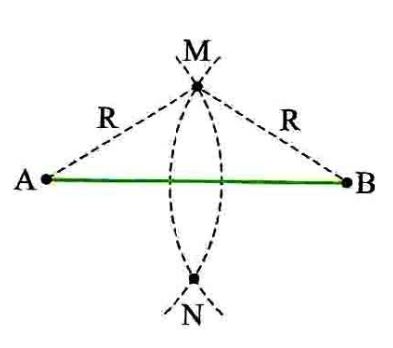
کاربرد اول) پیدا کردن نقاط با فاصله خاص از دو نقطه: اگر دو نقطه A و B به فاصله L از هم قرار داشته باشند، می توانیم نقاطی پیدا کنیم که به فاصله مساوی از A و B قرار داشته باشند. برای این منظور کافی است دهانه یک پرگار را به اندازه بزرگتر از باز کنیم و به مراکز A و B کمان هایی بزنیم. چون دهانه پرگار بیش از نصف طول پاره خط باز شده است، این کمان ها حتماً همدیگر را قطع می کنند و محل تقاطع آنها از A و B به یک فاصله ست.
یادتان باشد اگر دانه پرگار کمتر از L به روی ۲ باز شود، دو کمان همدیگر را قطع نمی کنند.
کاربرد دوم) پیدا کردن نقاطی به فاصله های متفاوت از دو نقطه: اگر دو نقطه A و B به فاصله L از هم قرار داشته باشند می توان نقاطی در صفحه یافت که به فاصله d1 از A و به فاصله d2 از B باشد. کافی است به مرکز A و به شعاع d1 و به مرکز B و به شعاع d2 دایره ای رسم کنیم. حال وضعیت این دو دایره نسبت به هم تعداد جواب های ممکن را به ما می دهد که چند حالت رخ می دهد:
- اگر دو دایره متقاطع باشند، مسئله دو جواب دارد.
- اگر دو دایره متخارج یا متداخل باشند، مسئله جواب ندارد.
- اگر دو دایره مماس خارج یا داخل باشند مسئله یک جواب دارد.
برای درک بهتر یک بار دیگر به شکل های وضعیت دو دایره نگاه کنید.
ببنید: تقارن چرخشی در ریاضی
رسم مثلث در ترسیم های هندسی
اگر اضلاع مثلثی a، b و c باشند، برای رسم آن باید ابتدا پاره خطی به طول a رسم کنیم. مانند BC؛ سپس دهانه پرگار را به اندازه b باز کرده و به مرکز C کمانی می زنیم و بار دیگر دهانه پرگار را به اندازه ی c باز کرده و به مرکز B کمانی می زنیم. اگر این کمان ها همدیگر را قطع کنند محل تقاطع آنها رأس A از مثلث ABC است.
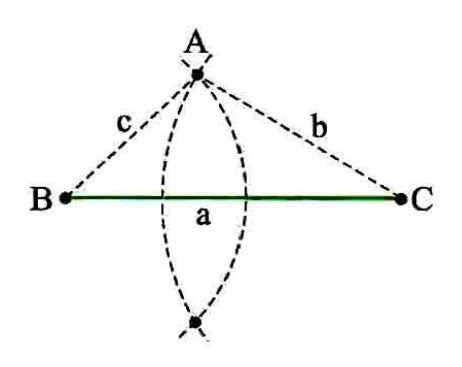
همان طور که در شکل می بینید، اگر کمان ها متقاطع باشند در دو نقطه همدیگر را قطع می کنند و به ظاهر به نظر می رسد که، دو مثلث متفاوت به دست می آید، اما اگر دقت کنید متوجه می شوید اضلاع مثلث دوم هم همین a،b و c است یعنی دو مثلث قابل انطباق یا همنهشت یا به بیان ساده تر شبیه یکدیگر هستند. یعنی تنها یک مثلث با این اضلاع وجود دارد.
حال سؤال این است که در چه صورتی با سه ضلع معلوم یک مثلث قابل رسم است؟
راه های هیجان انگیز
قضیه وجود مثلث: در صورتی یک مثلث به اضلاع a، b و c وجود دارد که هر ضلع آن از مجموع دو ضلع دیگر کوچکتر باشد. یعنی اگر a>b>c باشد باید بزرگ ترین ضلع مثلث از مجموع دو ضلع دیگر کوچکتر باشد.
A<b+c
اما اگر ندانیم کدام ضلع کوچکتر یا بزرگتر است یعنی اضلاع پارامتری باشند دو حالت رخ می دهد:
- تنها یک ضلع پارامتری است: اگر یک ضلع مثلث مجهول و دو ضلع دیگر معلوم باشد در صورتی این مثلث قابل رسم است که ضلع مجهول بین تفاضل و جمع دو معلوم باشد. یعنی:
|b-c|<a<b+c
- بیش از یک ضلع پارامتری است: اگر دو ضلع یا هر سه ضلع مثلث بر حسب پارامتر داده شده بود مثلاً a و 1+a2 و 5-a3 برای این که ببینیم مقدار پارامتر چه چیزی باید باشد تا مثلث قابل رسم شود، باید هر کدام از اضلاع را از مجموع دو ضلع دیگر کوچکتر قرار دهید و از نامساوی های بدست آمده اشتراک بگیرید.
نکته: اگر سه عدد داده شده یا با آن ها مثلثی رسم نمی شود یا اگر رسم شود تنها یک مثلث قابل رسم است. در واقع مثلث های دیگر در صورت وجود قابل انطباق و همنهشت با همنهشت مثلث هستند.
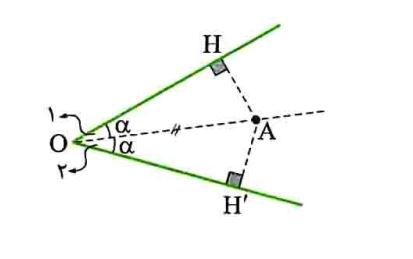
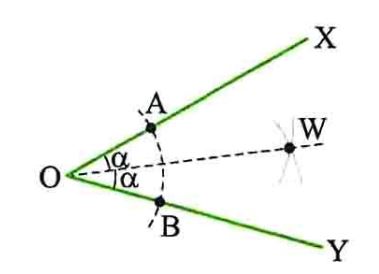
برخی خواص نیمساز و ترسیم آن: کم و بیش با واژه نیمساز آشنایی دارید. نیمساز هر زاویه نیم خطی است که از رأس زاویه رسم می شود و زاویه را به دو قسمت مساوی تقسیم می کند. حال به یکی از خاصیت های مهم نیمساز می پردازیم:
- خاصیت نیمساز: هر نقطه که روی نیمساز یک زاویه قرار داشته باشد از دو ضلع به یک فاصله است و برعکس هر نقطه که از دو ضلع زاویه به یک فاصله باشد روی نیمساز آن زاویه قرار دارد.

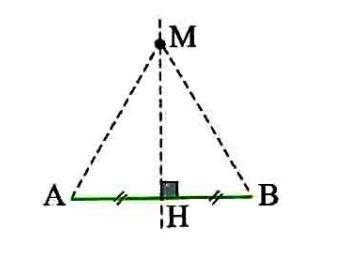
برخی خواص عمود منصف و ترسیم آن: عمود منصف هر پاره خط، خطی است که بر آن پاره خط عمود است و آن را نصف می کند. حال به یکی از خاصیت های مهم عمود منصف می پردازیم:
خاصیت عمود منصف: هر نقطه که روی عمود منصف یک پاره خط باشد از دو سر پاره خط به یک فاصله است و برعکس هر نقطه که از دو سر یک پاره خط به یک فاصله باشد روی عمود منصف پاره خط واقع است.
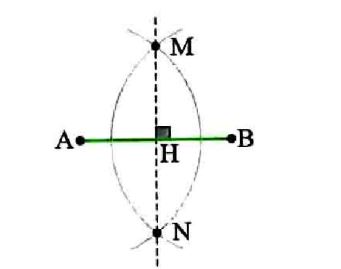
ترسیم عمود منصف: برای رسم عمود منصف پاره خط AB دهانه پرگار را بیش از نصف طول AB باز می کنیم و یک بار به مرکز A و یک بار به مرکز B کمان هایی رسم می کنیم. سپس محل تقاطع های این کمان ها را به هم وصل می کنیم چون نقاط M و N هم از A و هم از B به یک فاصله اند روی عمود منصف AB قرار دارند.
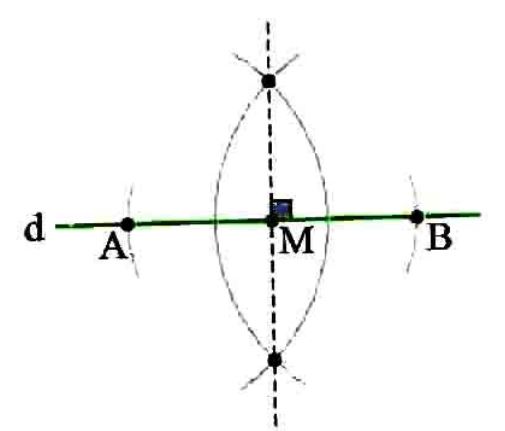
رسم خط عمود بر یک خط از نقطه ای واقع بر آن: فرض کنیم نقطه M روی خط d قرار دارد و می خواهیم به کمک خط کش و پرگار خطی عمود بر d و گذرا از M رسم کنیم. کافی است به مرکز M و به شعاع دلخواه کمانی بزنیم تا خط d را در A و B قطع کند. حال کافی است عمود منصف پاره خط AB را طبق آنچه یاد گرفتیم رسم کنیم.
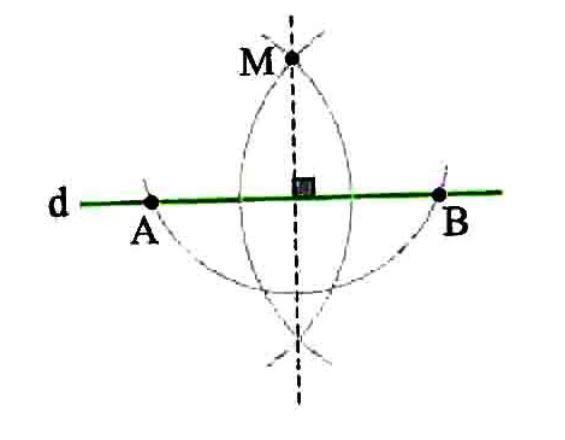
رسم خط عمود بر یک خط از نقطه ای خارج از آن: فرض کنید نقطه M خارج d باشد، برای رسم خطی که از M بگذرد و بر d عمود باشد، کافی است به مرکز M و به شعاع دلخواه کمانی بزنیم، طوری که خط d را در نقطه های A و B قطع کند. حال عمود منصف پاره خط AB را رسم می کنیم که از M می گذرد .(چون BM=AM است M روی عمود منصف خواهد بود.)
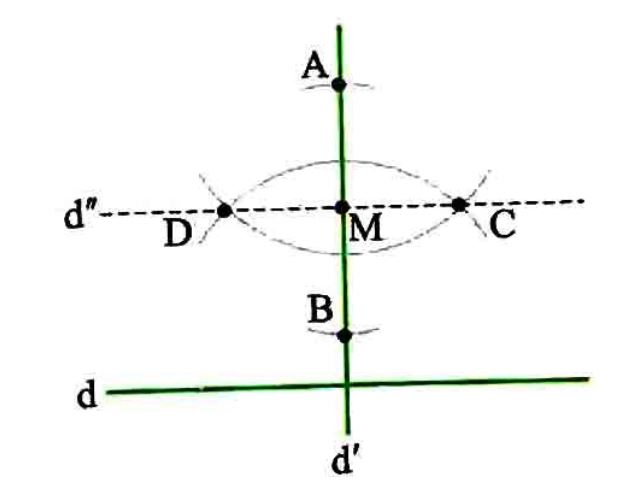
رسم خطی موازی با یک خط از نقطه ای خارج از آن: فرض کنید M خارج از خط d قرار دارد، می خواهیم خطی از M عبور دهیم که موازی d باشد. ابتدا طبق آنچه گفتیم خطی گذرا از M و عمود بر d رسم می کنیم و آن را d’ می نامیم، حال نقطه M واقع بر d’ است. حالا دوباره خطی گذرا از M و عمود بر d’ رسم می کنیم و آن را d’’ می نامیم، در نتیجه d’’||d خواهد بود.
پیدا کردن نقاطی به فاصله k از یک خط: خط d مطابق شکل مفروض است.
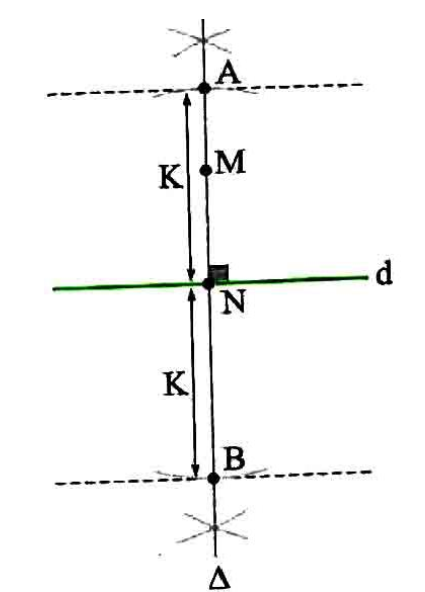
فرض کنید می خواهیم نقاطی را پیدا کنیم که به فاصله k واحد از این خط قرار دارند، کافی است نقطه ای دلخواه مانند M خارج آن در نظر بگیریم و طبق شرایط گفته شده خط عمود بر d و گذرا از M (که آن را ∆ می نامیم) را رسم کنیم تا خط d را در N قطع کند. حال به مرکز N و به شعاع k کمانی می زنیم تا این خط عمود را در A و B قطع کند. مجدداً از نقاط A و B واقع بر خط ∆ عمود هایی بر آن رسم می کنیم. این دو خط شامل همه نقاطی هستند که به فاصله k واحد از خط d قرار دارند.
همچنین شاید مفید باشد: تقسیم چند جمله ای











دیدگاهتان را بنویسید