آموزش تعیین علامت در ریاضی

آموزش تعیین علامت در ریاضی | در این بخش قصد داریم ادامه فصل چهارم ریاضی دهم و مبحث تعیین علامت را بررسی کنیم به این دلیل که این مبحث بسیار مهم است و در سال های یازدهم و دوازدهم با آن ها سر و کار زیادی خواهیم داشت.

در کتاب درسی، تعیین علامت درجه یک و درجه دو، یعنی معادله درجه یک و درجه دوم را تدریس کرده است.

آموزش تعیین علامت 😃

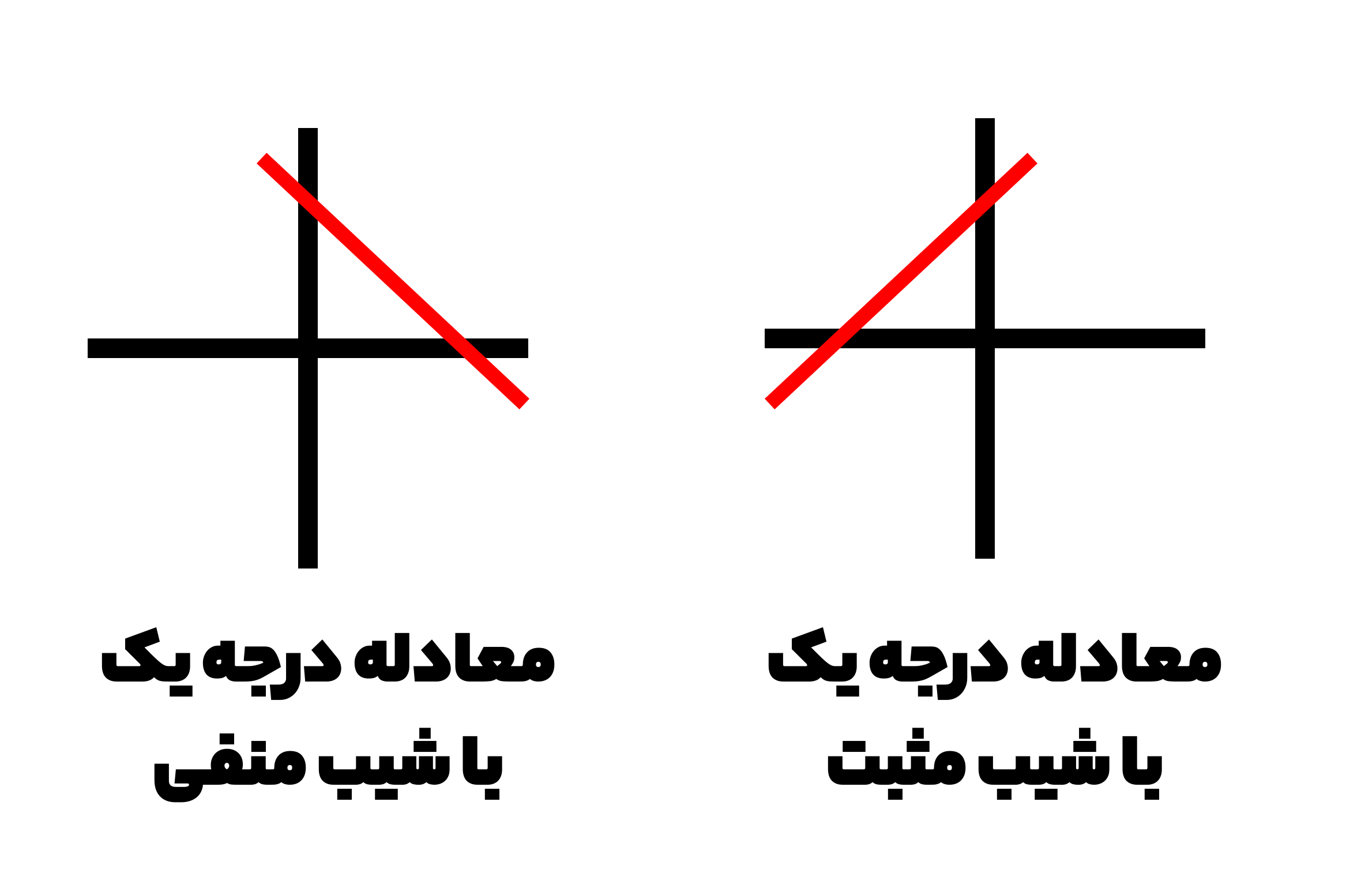
در نظر داشته باشید که وقتی خط را رسم می کنید محور x و y را قطع می کند:

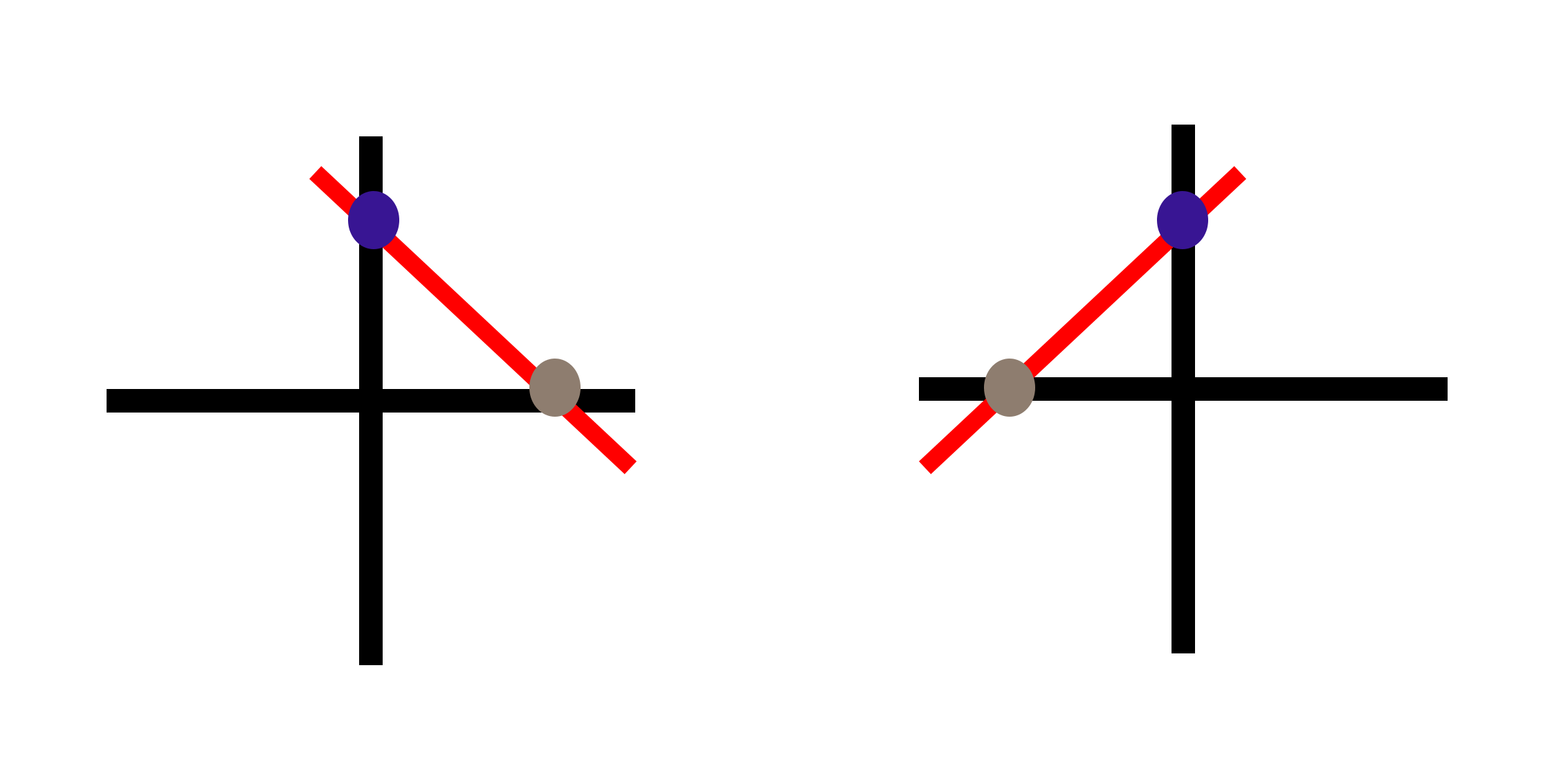
در محور مختصاتی سمت چپ، خط ترسیم شده سر پایینی است و از بالا به پایین است در نتیجه دارای یب منفی خواهد بود و در محور مختصات سمت راست، خط ترسیم شده سر بالایی است و از پایین به بالا است که شیب آن مثبت خواهد شد:

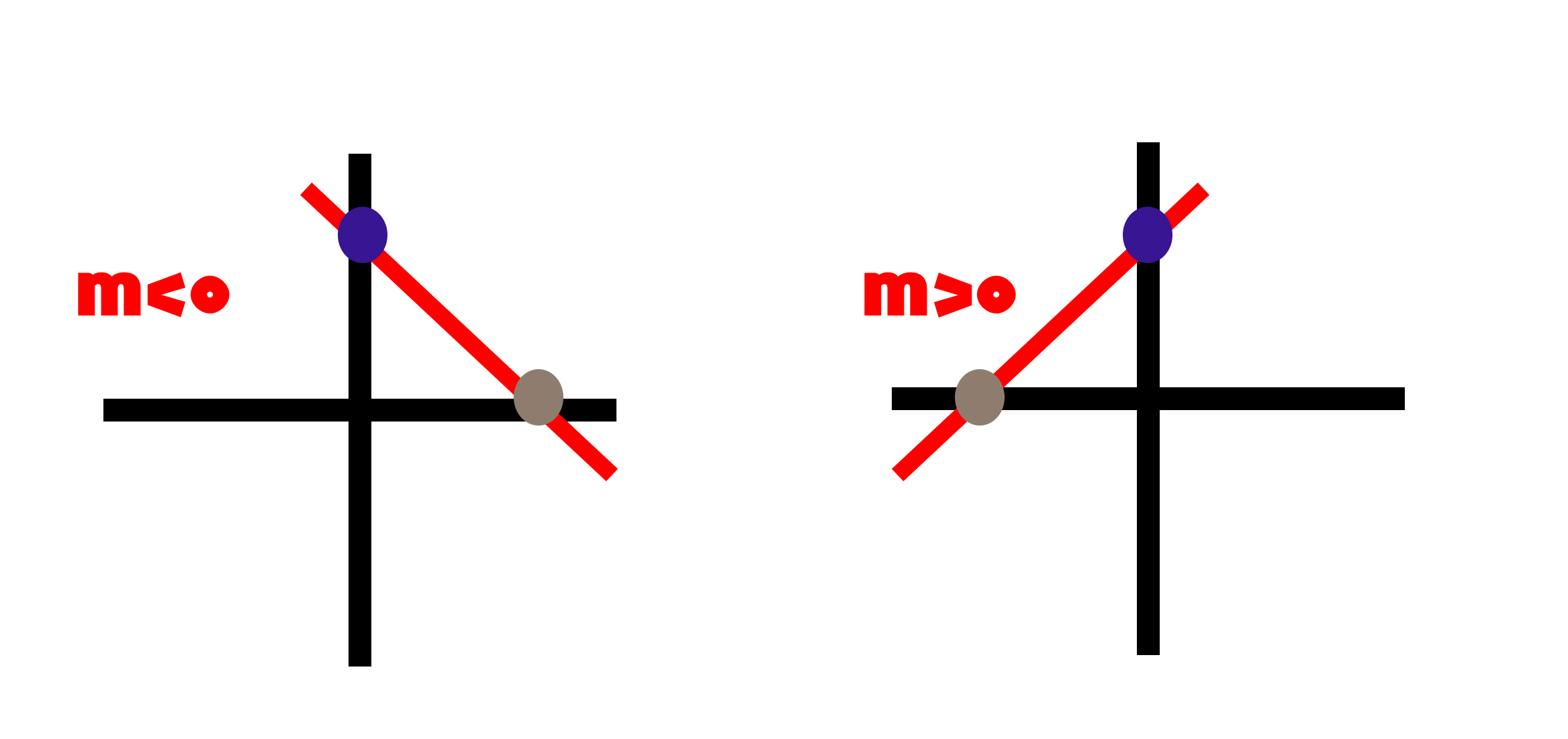
سؤالی که همیشه به وجود می آید این است که وقتی می گوییم تعیین علامت مگر چند نوع علامت داریم؛ اکثریت می گوییم علامت مثبت و علامت منفی. این موضوع کاملاً درست است اما ما باید یک خط مرز را در نظر بگیریم و بگوییم از یک جا به بالا و از یک جا به پایین.

اتفاق رایجی که بین دانش آموزان وجود دارد این است که وقتی گفته می شود یک عبارت را تعیین علامت کن، دانش آموز x ها را تعیین علامت می کند، یادتان باشد که x تکلیف مشخصی دارد و علامت آن مشخص است، یا در قسمت مثبت هاست یا در قسمت منفی ها و یا صفر است.

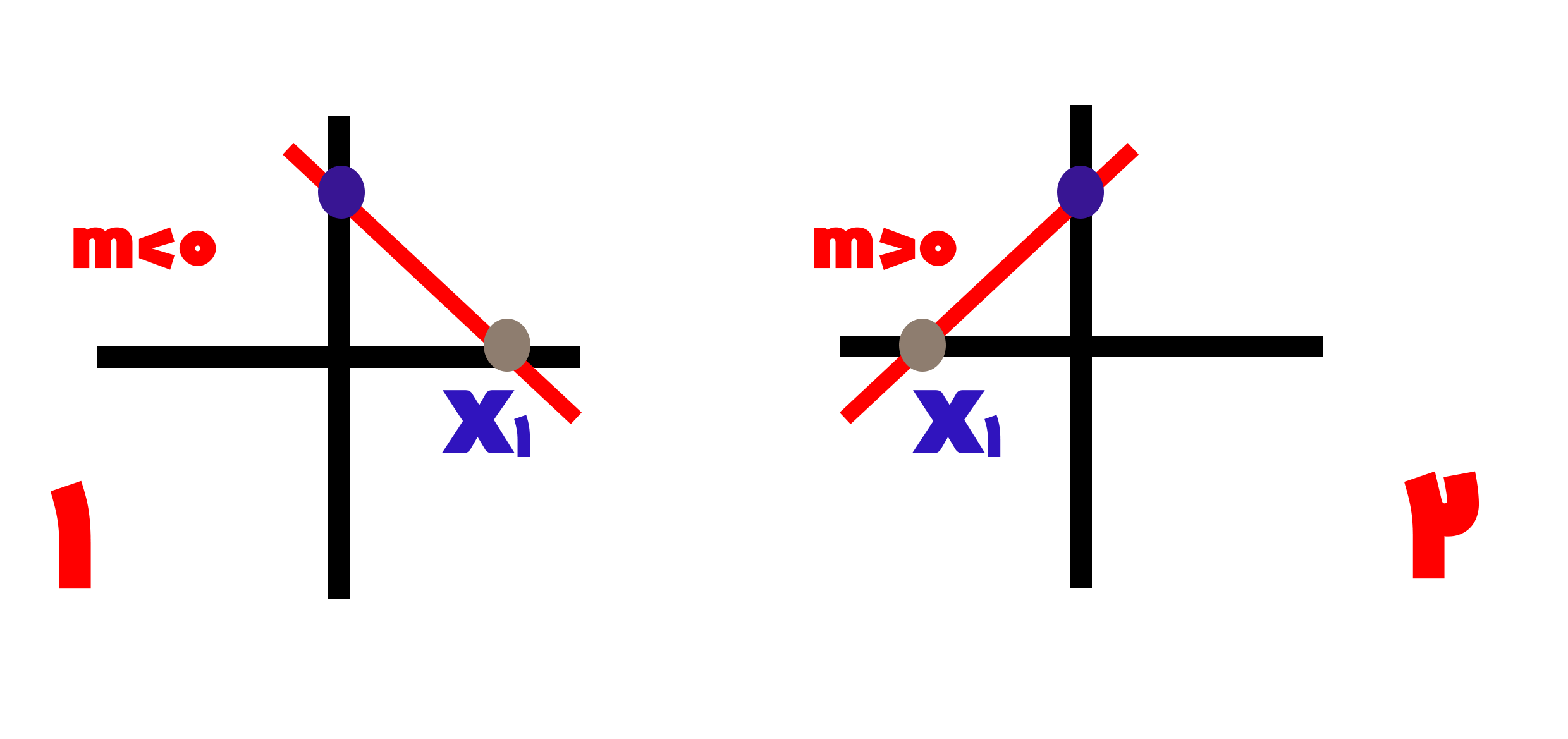
در شکل شماره 1، از ریشه یا نقطه x₁، به پایین نمودار شما زیر محور x هاست، در نتیجه y منفی به شما می دهد و همچنین از ریشه به بالا، نمودار شما y ها را در قسمت مثبت نشان می دهد و در نقطه x₁، محور y ها صفر را به شما نشان می دهد.

در شکل شماره 2، در نقطه ای که ریشه در آن قرار دارد، محور y ها صفر را نشان می دهد، زیر ریشه محور y ها منفی و بالای ریشه محور y ها مثبت است.

در نظر داشته باشید نقطه ای که محور y ها را قطع کرده است، عرض از مبدأ ما خواهد بود و در واقع همان ارتفاع ما است که در تعیین علامت نقشی ندارد

در تعیین علامت، نقش اصلی را ریشه ها ایفا می کنند

در کتاب درسی، یک فرمول عنوان کرده است که اگر یک معادله درجه اول دیدید:

y = ax+b

اول از همه ریشه این معادله را بدست بیاورید، یعنی اینکه y را مساوی صفر قرار دهید:

y=ax+b=>y=0

در نتیجه سمت راست تساوی نیز برابر با صفر می شود:

ax+b=0=>x=(-b)/a(ریشه)

در کتاب جدول تعیین علامت را بصورت زیر مشخص کرده است، جدولی که احتیاجی به حفظ کردن ندارد و مفهوم آن در این بخش کاملاً برای شما جا می افتد:

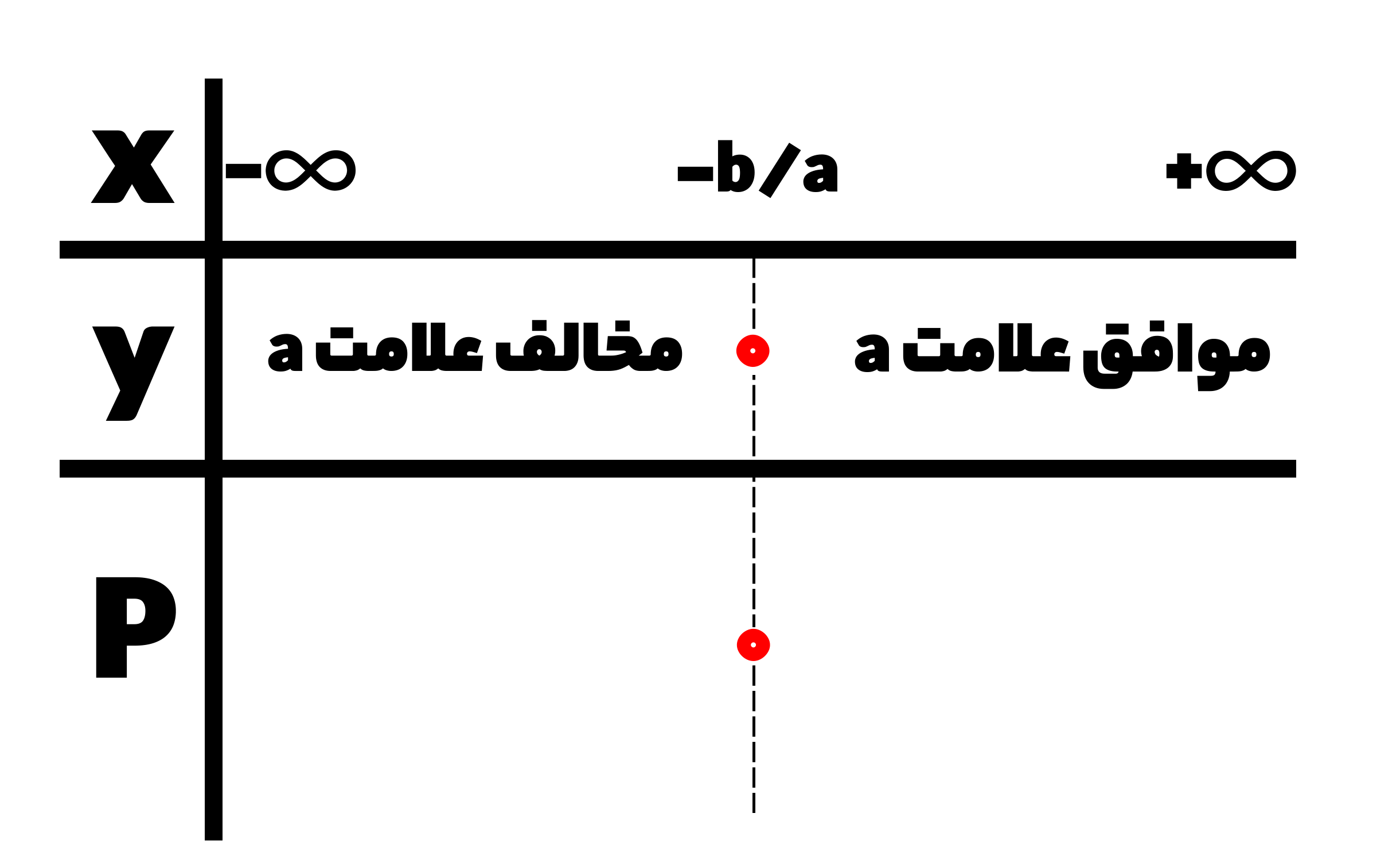
همان طور که مشاهده می کنید، در این جدول ریشه را از کوچک به بزرگ می نویسند و معادله درجه اول هم یک ریشه بیشتر ندارد که همان (-b)/a  می باشد. نقطه چینی که در قسمت ریشه گذاشته می شود دقیقاً نشان دهنده همان نقطه ای است که ما روی مرز هستیم و در این نقطه خاص تابع و تعیین علامت ما صفر است، یعنی این ریشه باعث میشه که تابع ما صفر شود. منظور از P در این جدول نیز همان تعیین علامت است.

اکنون به سراغ شکل شماره 1 می رویم و می خواهیم آن را تعیین علامت کنیم:

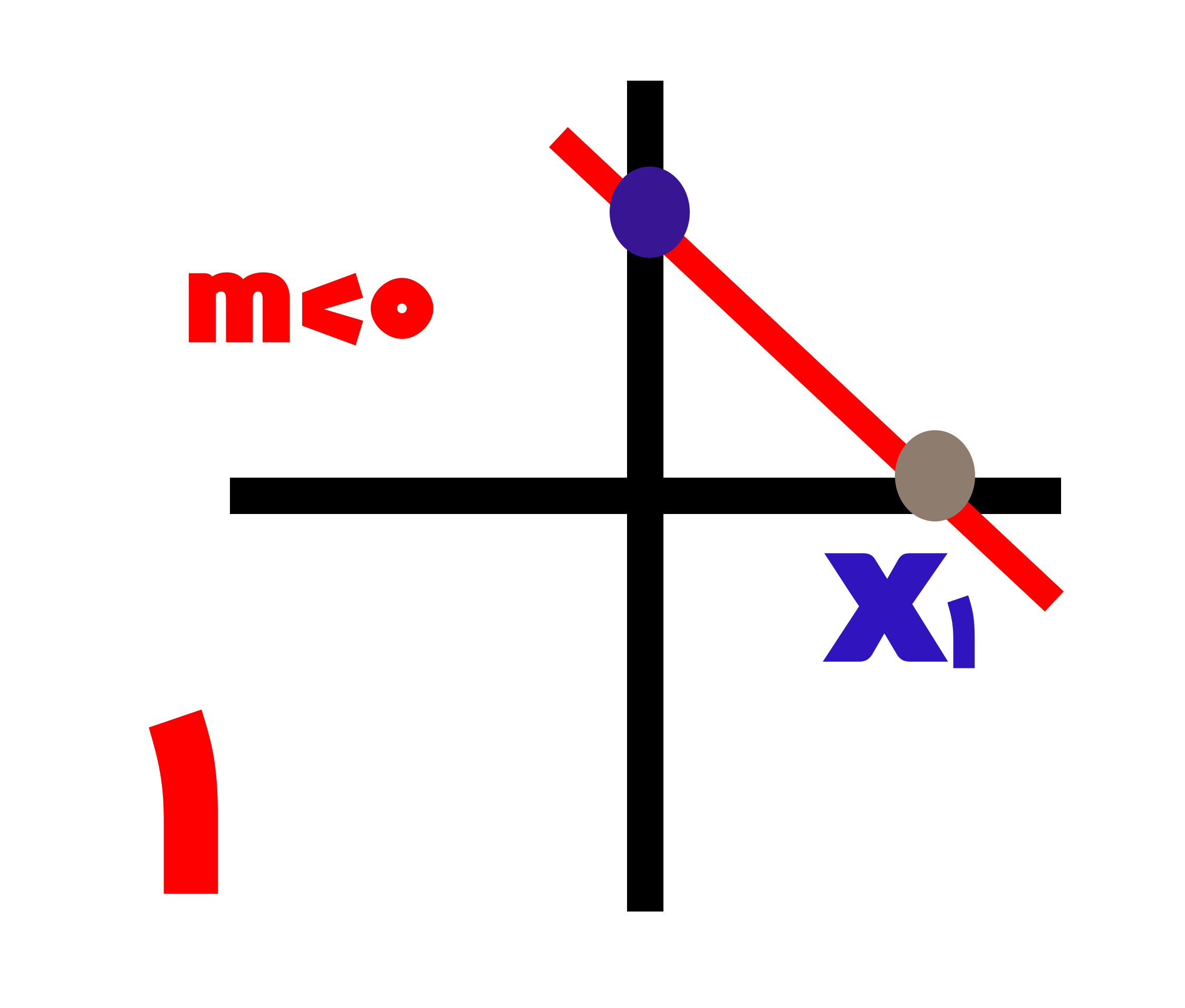
همان طور که مشاهده می کنید این معادله شیب منفی دارد که منظور از شیب همان a می باشد که در اینجا منفی است، پس در نتیجه تعیین علامت این معادله بصورت زیر است:

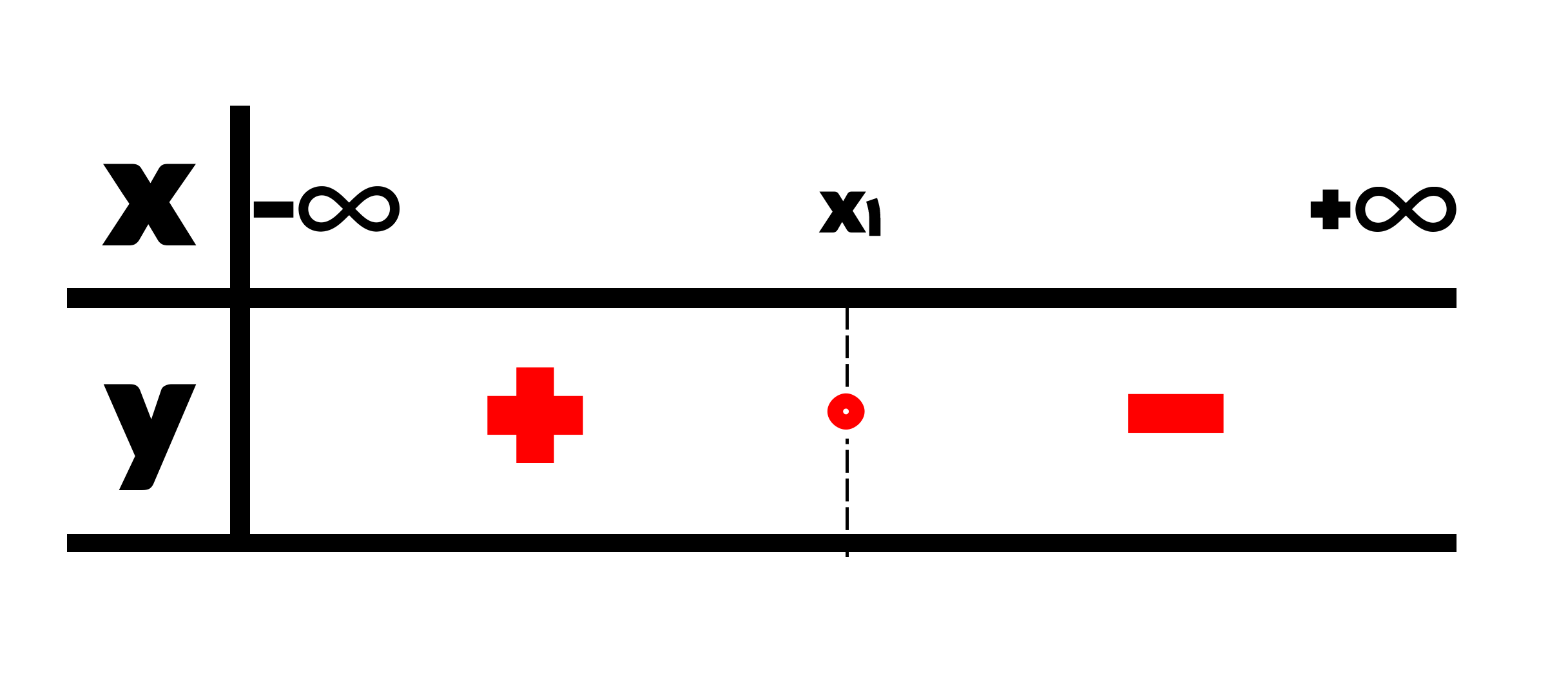
همان گونه که می بینید صفر همان ریشه است، از ریشه به جلو تر یعنی x₂، x₃ و … y را منفی می کنند اما قبل از ریشه y را مثبت می کنند.

حالا شکل شماره 2 را تعیین علامت می کنیم:

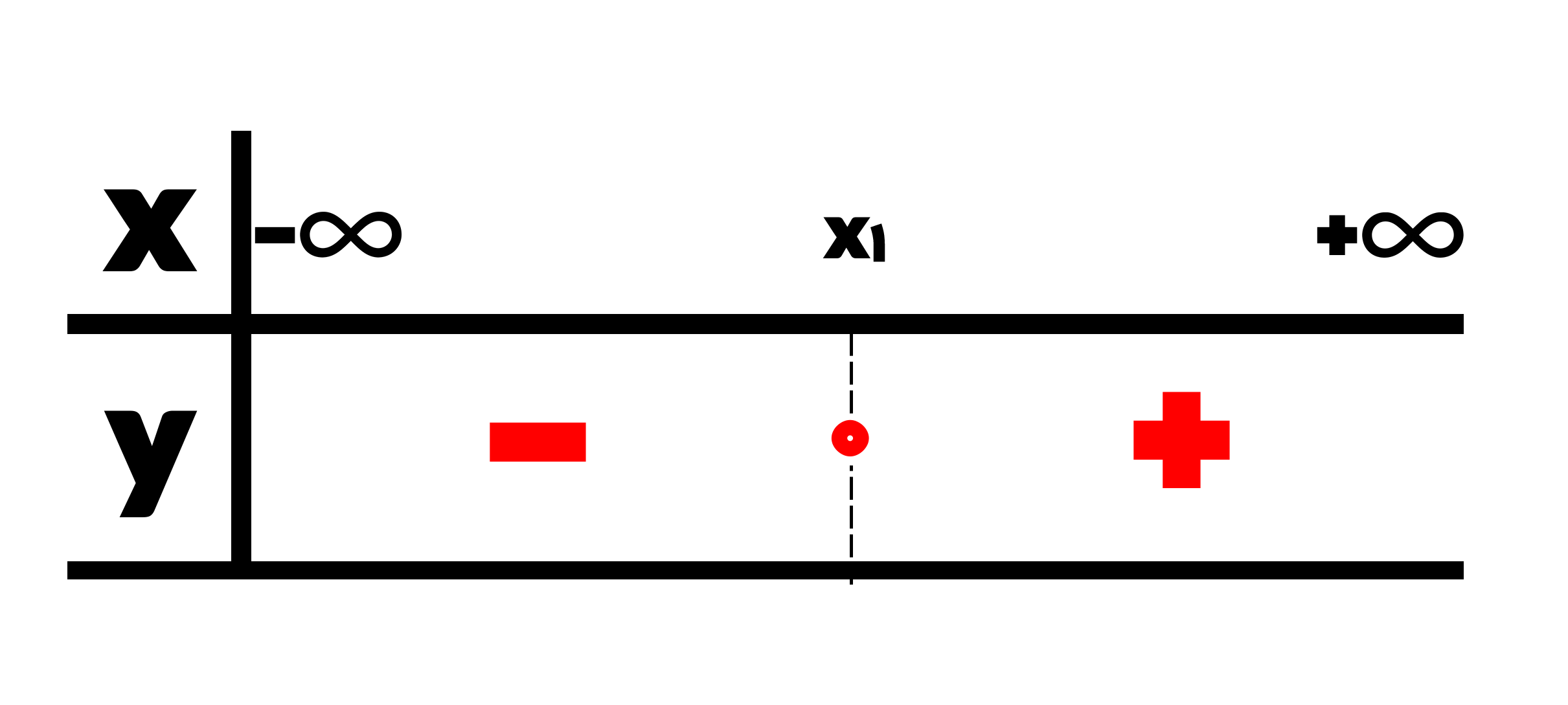
یک نکته را دقت کنید که چرا علامت نمودار درجه یک از مثبت به منفی و یا از منفی به مثبت در حال تغییر است. همان طور که همه ما قبول داریم x₁ ریشه است، هنگامی که نمودار از این ریشه می گذرد، علامت ها عوض می شود.

بنابراین توجه داشته باشید، هنگامی که نمودار از ریشه های ساده عبور می کند، علامت عوض می شود.

تعیین علامت معادله درجه دوم

سه معادله درجه 2 را بصورت فرضی رسم می کنیم:

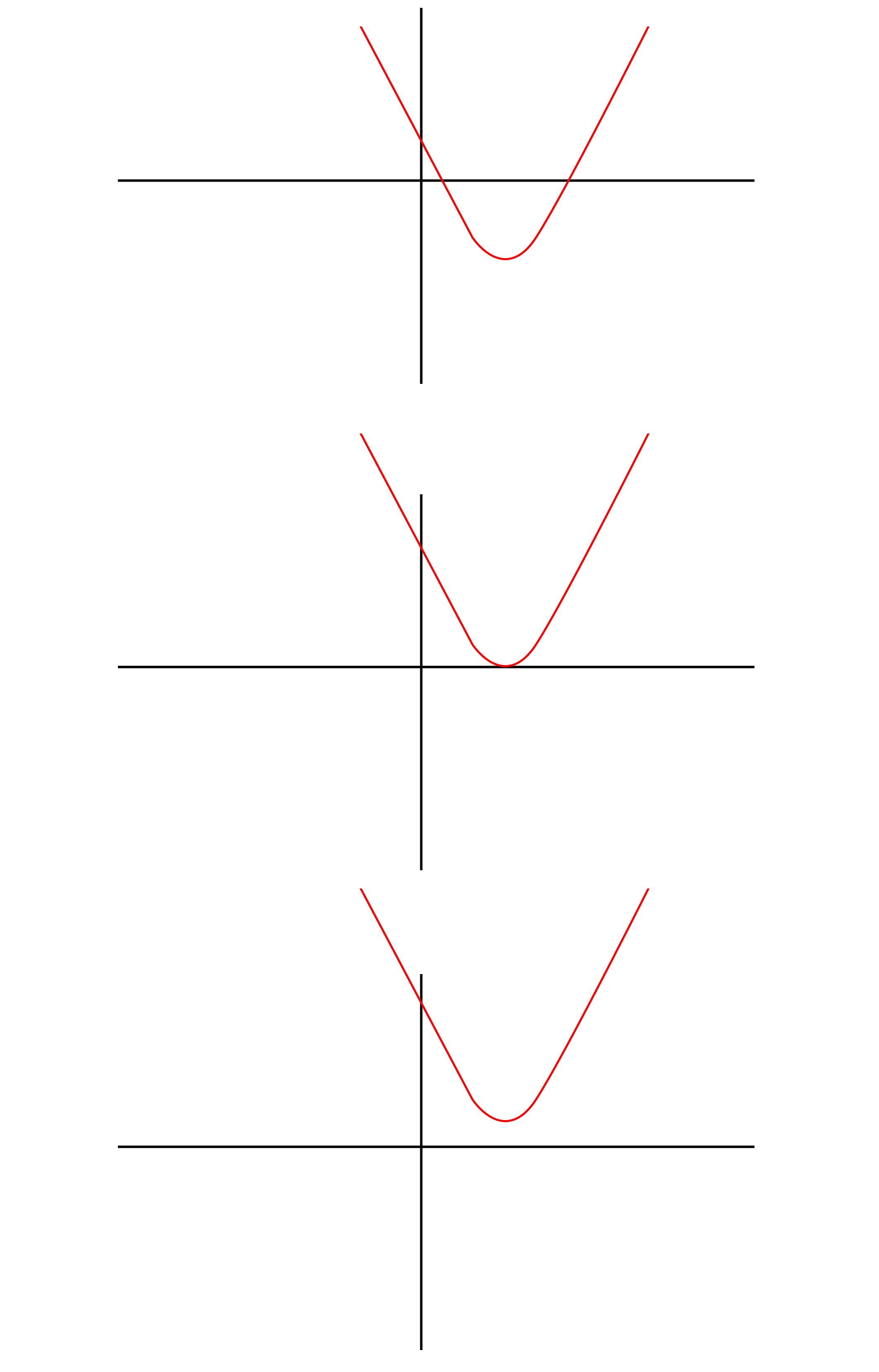
در ابتدا ریشه ها را روی هر نمودار مشخص می کنیم:

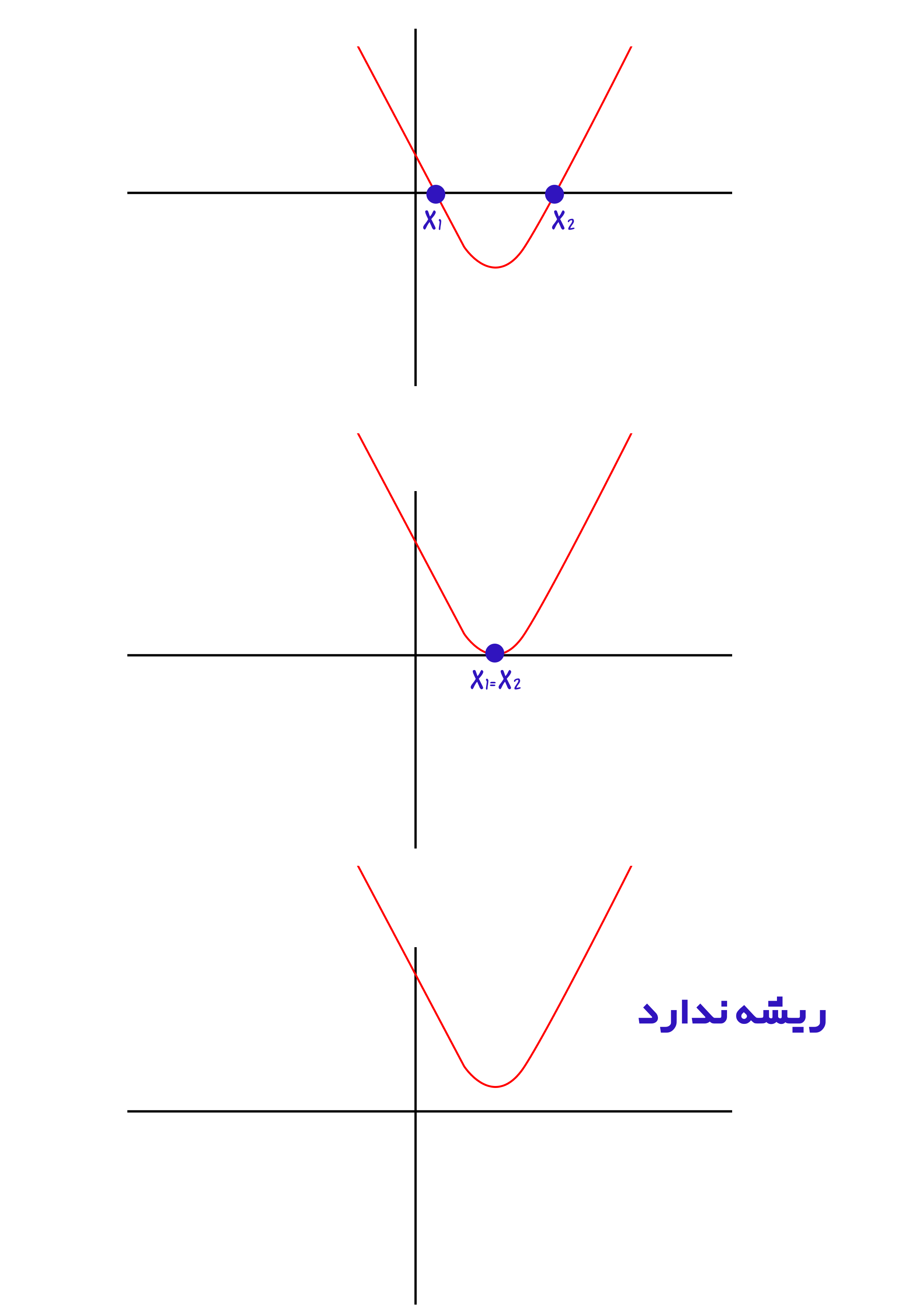
از لحاظ دلتا یز نمودار ها را بری می کنیم:

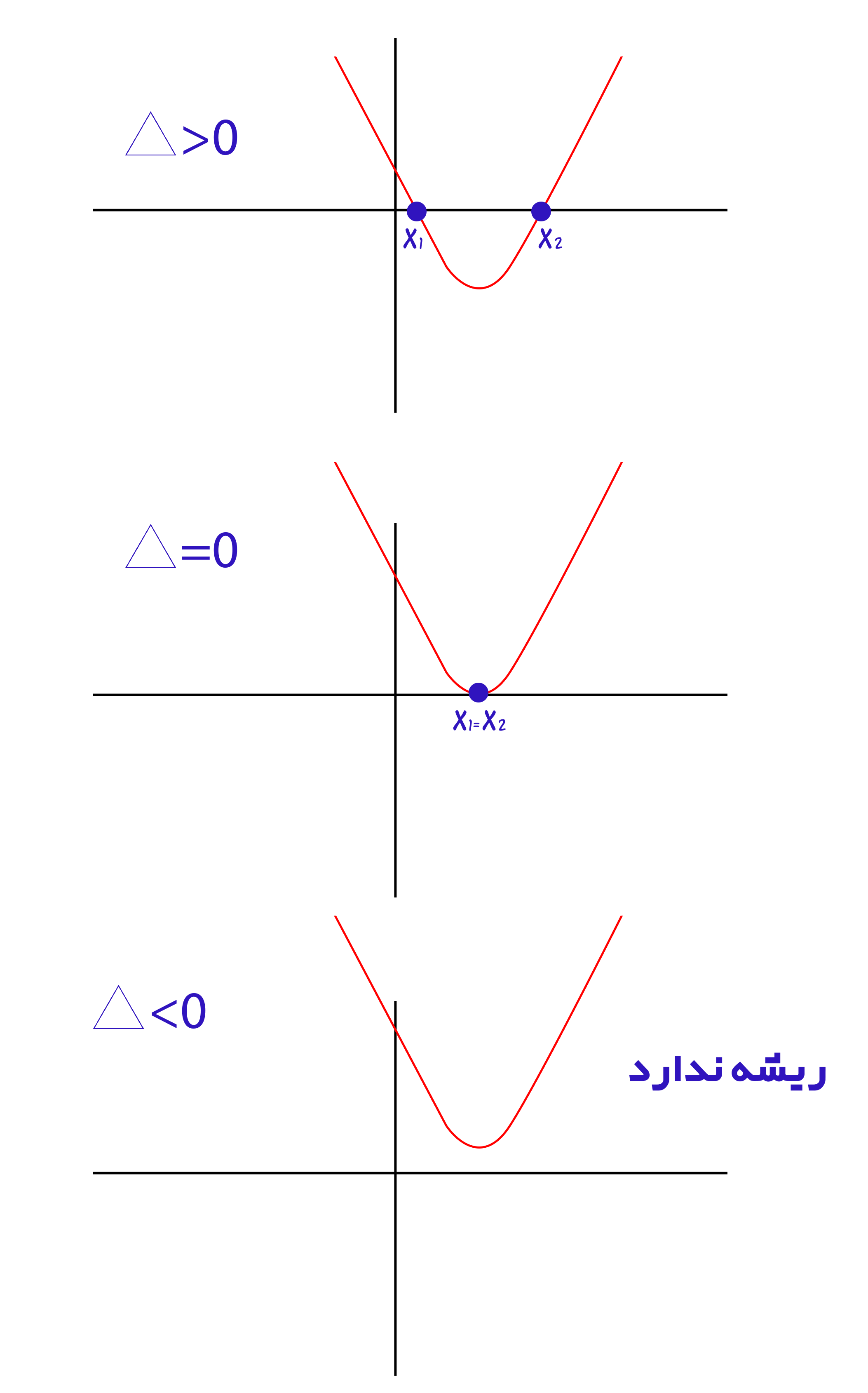
آموزش تعیین علامت سریع

پس نتیجه می گیریم که معادله درجه دوم از لحاظ دلتا، در سه حالت می باشد، که هر سه حالت را باید در نظر بگیریم. توجه داشته باشید که برای تعیین علامت نقاط عرض از مبدأ اهمیتی برای ما ندارند.

معادله درجه دوم را همه ی ما نسبت به آن اشراف داریم:

y=ax^2+bx+c

علت این که برای معادله درجه دوم سه شکل رسم کردیم این بود که جدول تعیین علامت آن نیز سه حالت دارد. در کتاب درسی اشاره کرده که اگر معادله ای درجه دو داشتید و خواستید آن را تعیین علامت کنید، طبق جدول زیر عمل کنید:

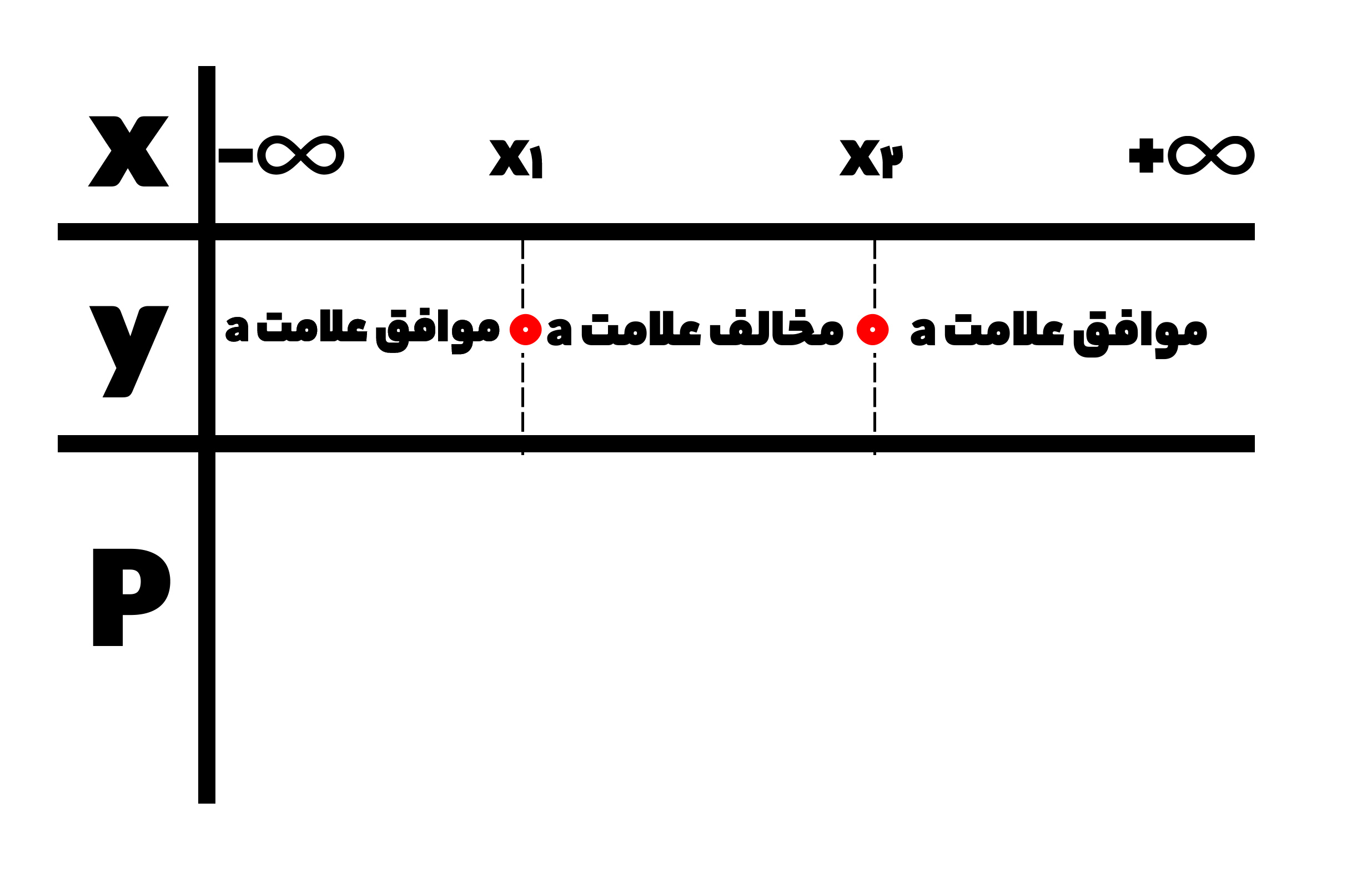
همان طور که مشاهده می کنید بین دو ریشه را باید مخالف علامت a باشد و قبل و بعد ریشه ها نیز موافق علامت a باید در نظر گرفته شود.

به سه نموداری که ترسیم کردیم، مجدداً دقت فرمایید:

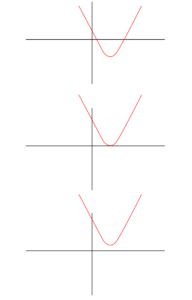
در هر سه نمودار شیب مثبت است، به این علت که هر سه رو به بالا هستند:

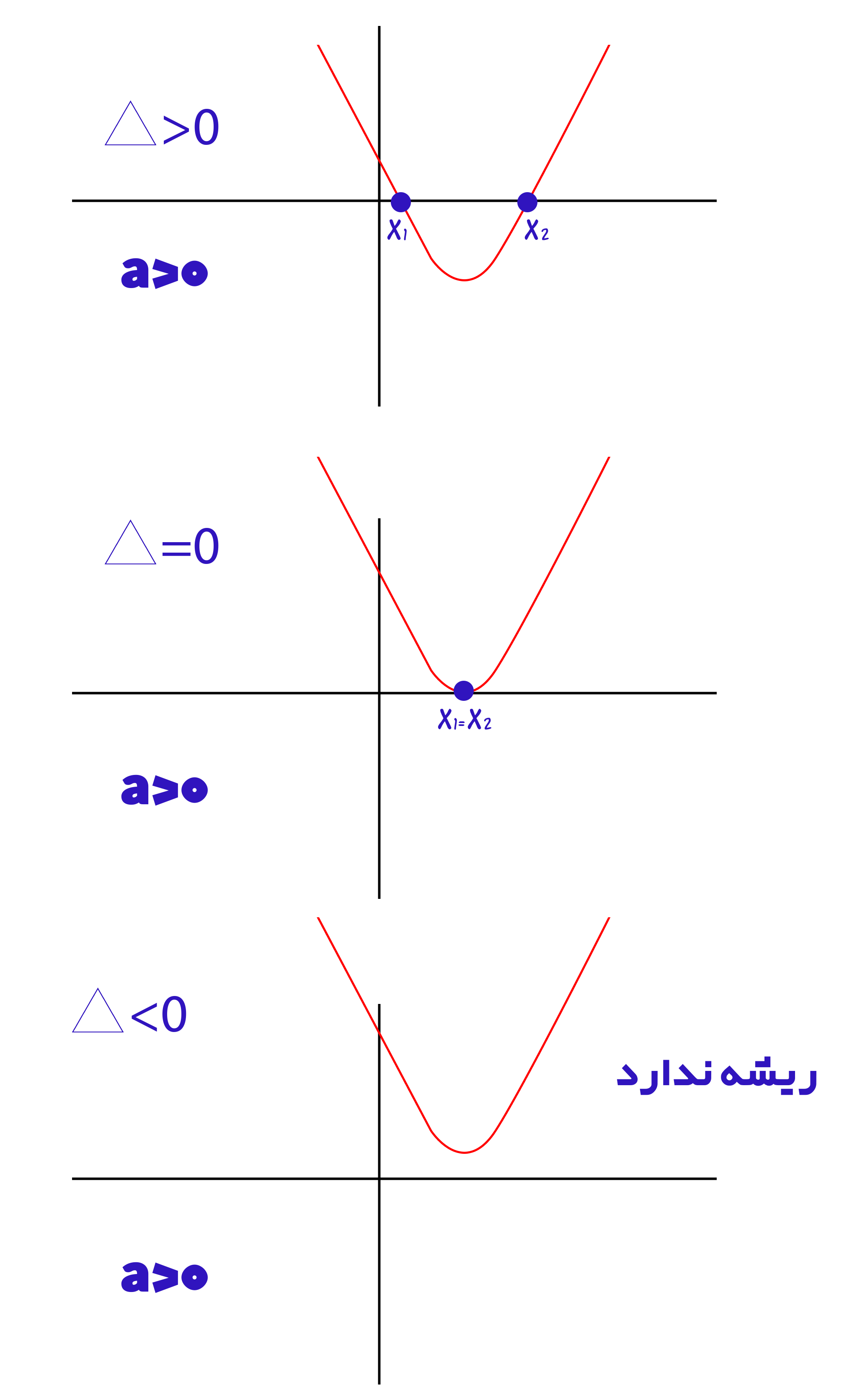
در نتیجه با توجه به علامت a، جدول تعیین علامت در حالتی که ∆>0 باشد، به شکل زیر خواهد بود:

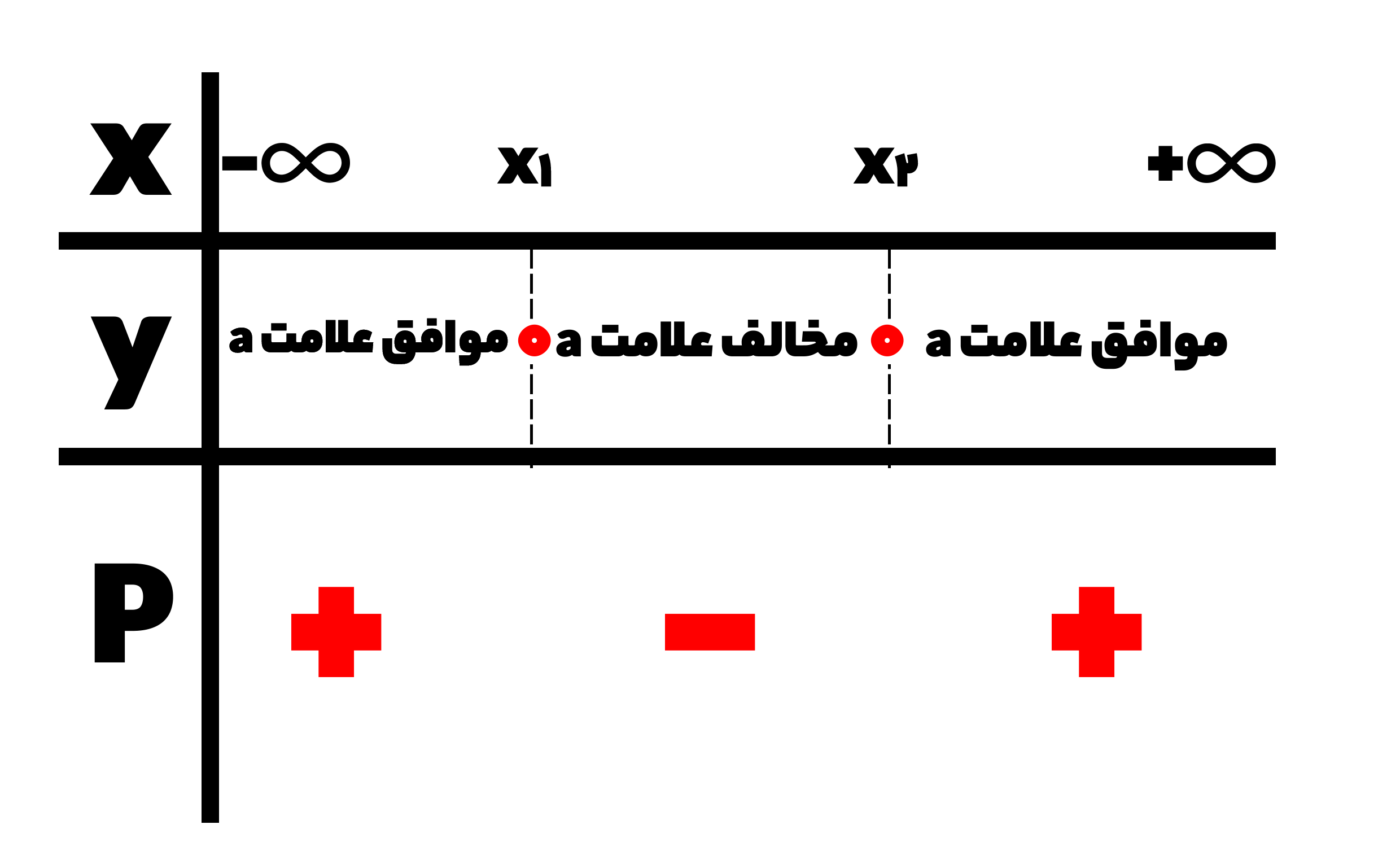
اگر به نمودار شماره یک نیز دقت کنید نقاط بین دو ریشه زیر محور x قرار گرفته اند، در نتیجه منفی هستند و نقاط قبل و بعد ریشه، بالای محور x ها هستند و در نتیجه مثبت خواهند بود. بنابراین نتیجه می گیریم هم طبق فرمولی که در کتاب عنوان شده و هم طبق نمودار تعیین علامت ها یکسان هستند.

همچنین ببینید: آموزش ریاضی دهم (صفر تا صد ریاضی دهم)

تعیین علامت تابع، در حالتی که 0=∆ باشد، به شکل زیر خواهد بود:

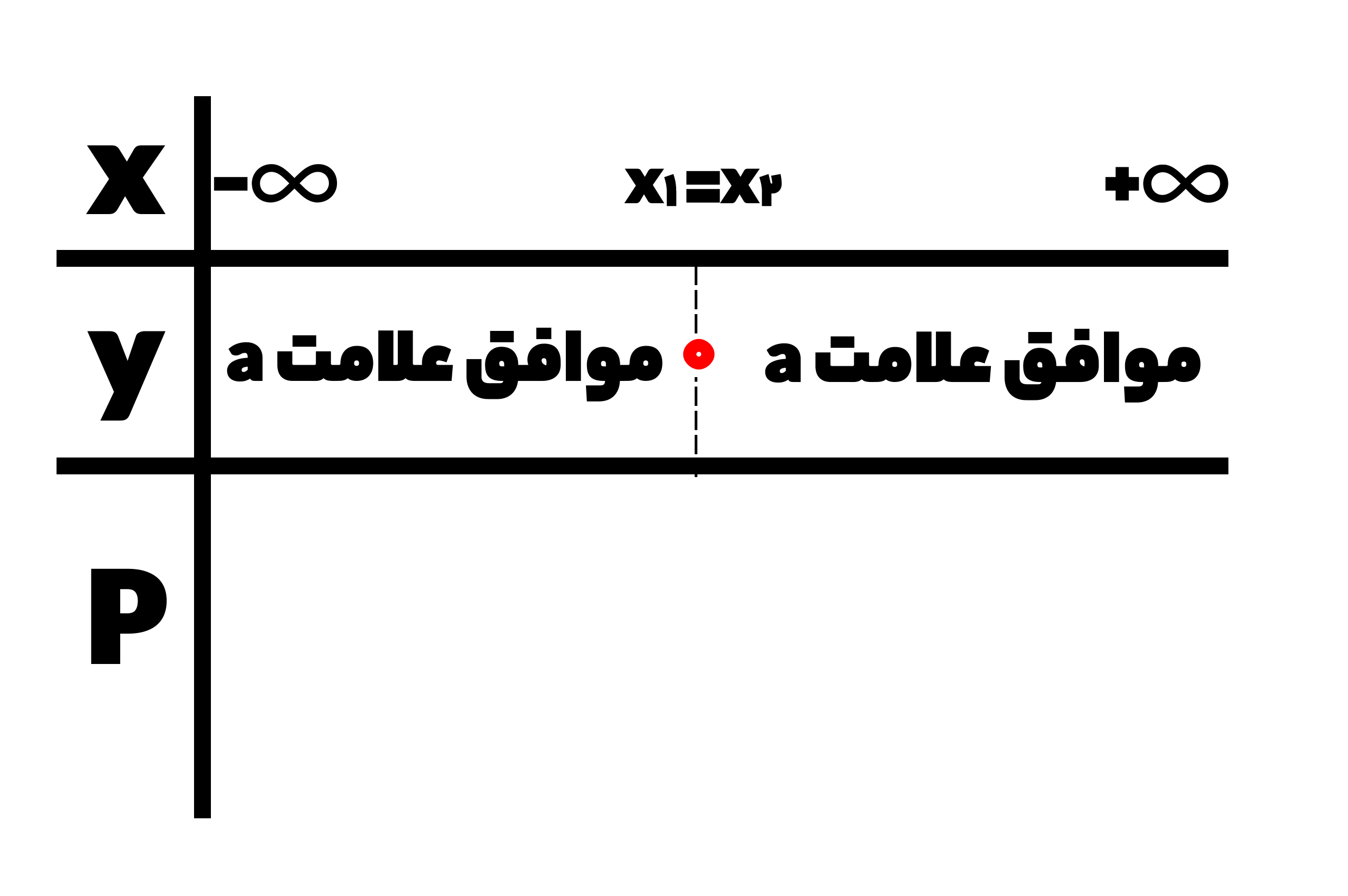
در نتیجه تعیین علامت نمودار شماره دو، بصورت زیر خواهد بود:

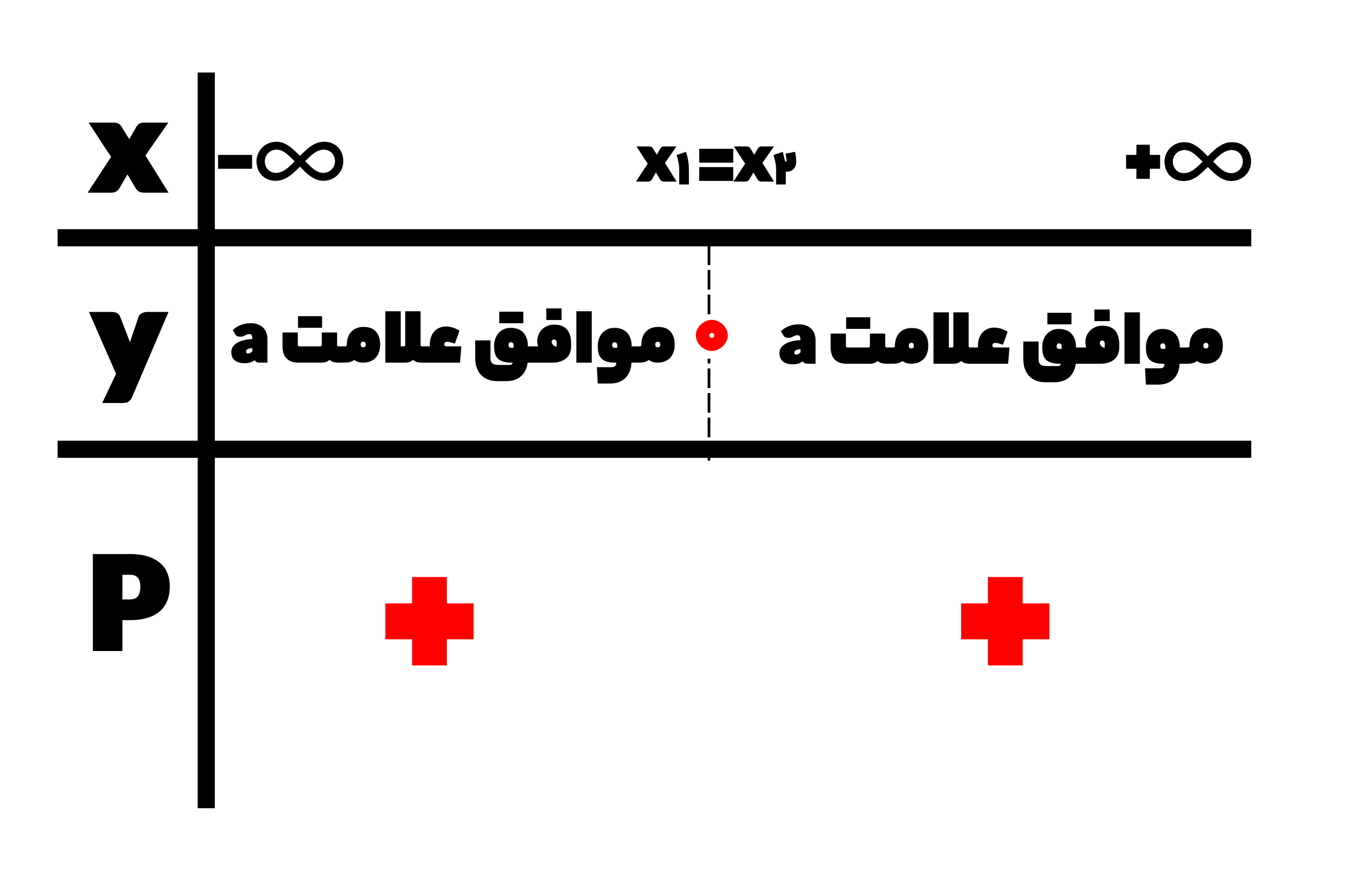
علت تغییر علامت در نمودار اول این است که همان طور که قبلاً اشاره کردیم، هنگامی که نمودار از ریشه رد می شود علامت تغییر می کند اما در نمودار دوم این اتفاق نمی افتد و نمودار به محض رسیدن به ریشه مجدداً رو به بالا حرکت می کند. در واقع در حالت دوم که نمودار مماس با ریشه می شود گفته می شود که “ریشه مضاعف” داریم.

در حالت سوم که 0<∆ می باشد، تعیین علامت بصورت زیر است:

در نتیجه تعیین علامت نمودار سوم نیز به قرار زیر است:

پس حواستان باشد که a در تعیین علامت همه کاره است. نکته ی دومی که باید به آن دقت کنید این است که a ضریب بزرگ ترین توان است.

کاربرد تعیین علامت

در اکثر اوقات کلمه تعیین علامت در کنار عبارت نامعادله قرار می گیرد. تابع زیر را در نظر بگیرید:

f(x)=x^2+5x+6

و از ما می خواهند تابع داده شده را، یا تعیین علامت کنیم و یا اینکه تابع را مثبت یا منفی در نظر بگیریم:

f(x)=x^2+5x+6≥0

هنگامی که یک عبارت دستوری را به ما می دهند مثل بزرگ تر یا مساوی صفر، یعنی این که قرار است قسمت هایی را انتخاب کنید که نمودار اصطلاحاً رو به بالا باشد یا اینکه مماس با محور x ها باشد.

در قدم اول به رسم همیشگی باید ریشه ها را بدست آورید. طبق تابع داده شده از اتحاد جمله مشترک استفاده می کنیم:

(x+2)(x+3)=0=> x_1=-2,x_2=-3

سپس جدول تعیین علامت را می کشیم. این نکته را در نظر بگیرید که بین دو ریشه مخالف علامت a خواهد بود و در این تابع a ضریب x² می باشد که 1+  است:

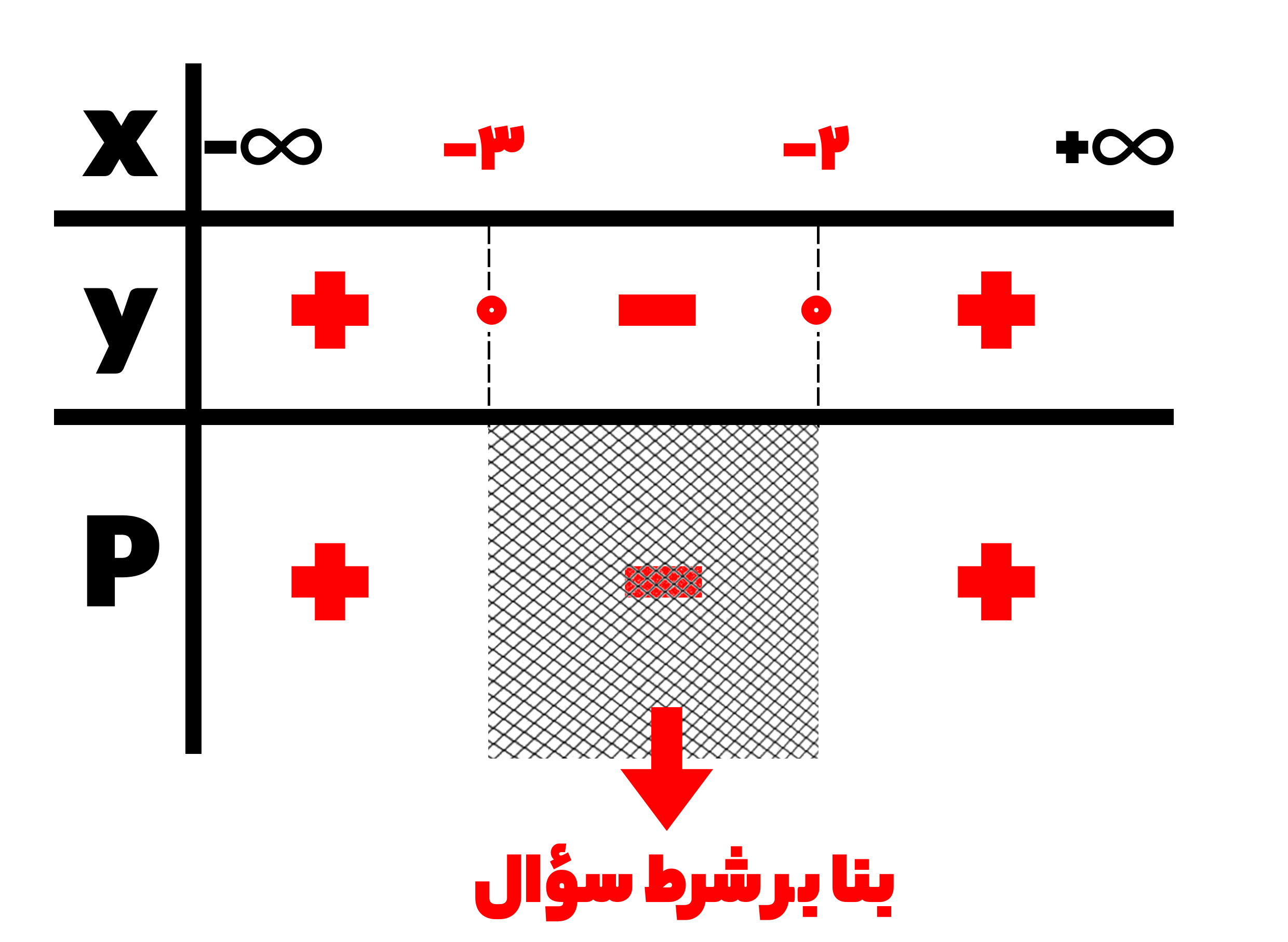
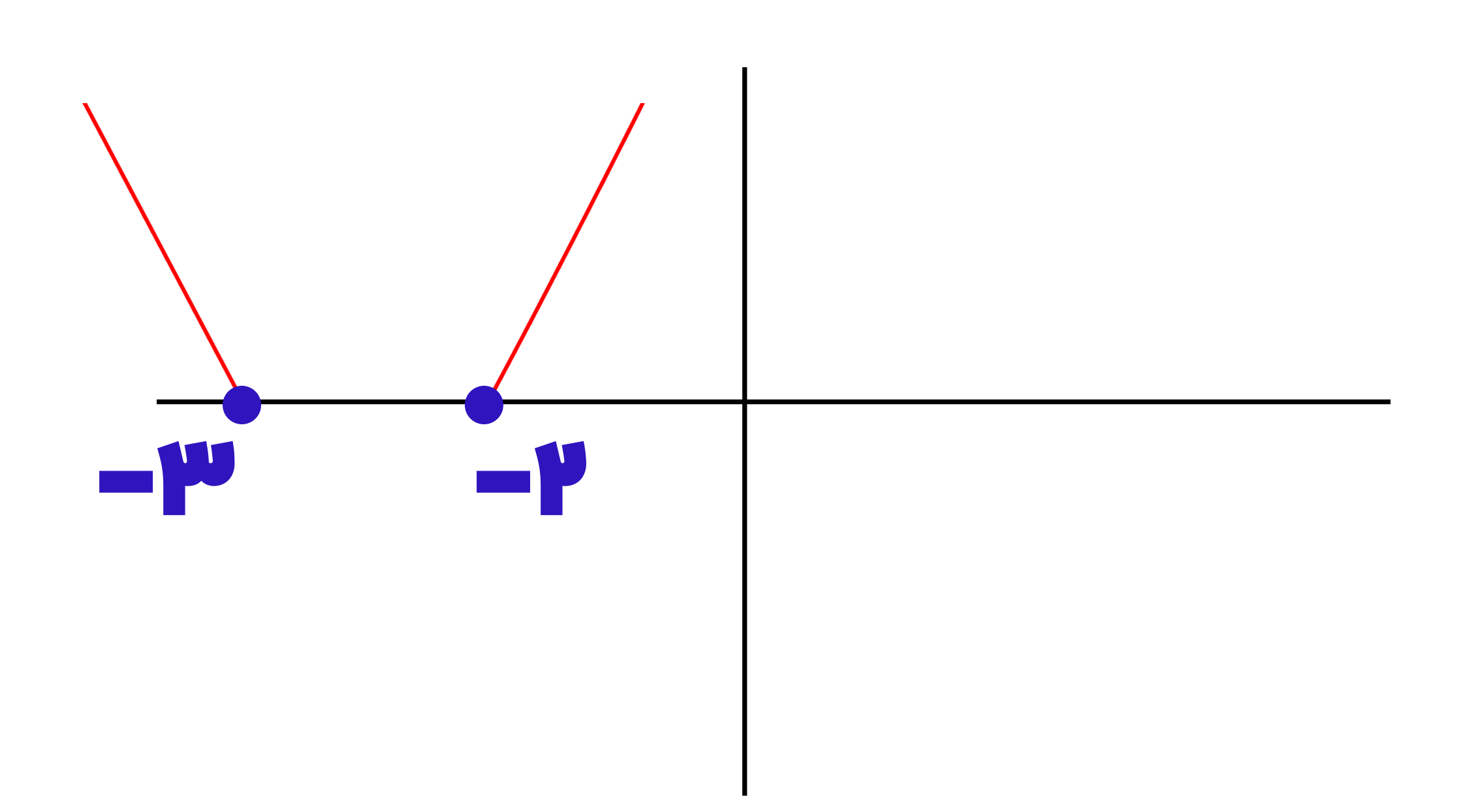
اکنون با توجه به همین تعیین علامت رسم آن را نیز می توانیم انجام دهیم. رای این کار ریشه ها را وی محور مختصات مشخص می کنیم و با توجه به جدول تعیین علامت نمودار سهمی را رسم می کنیم:

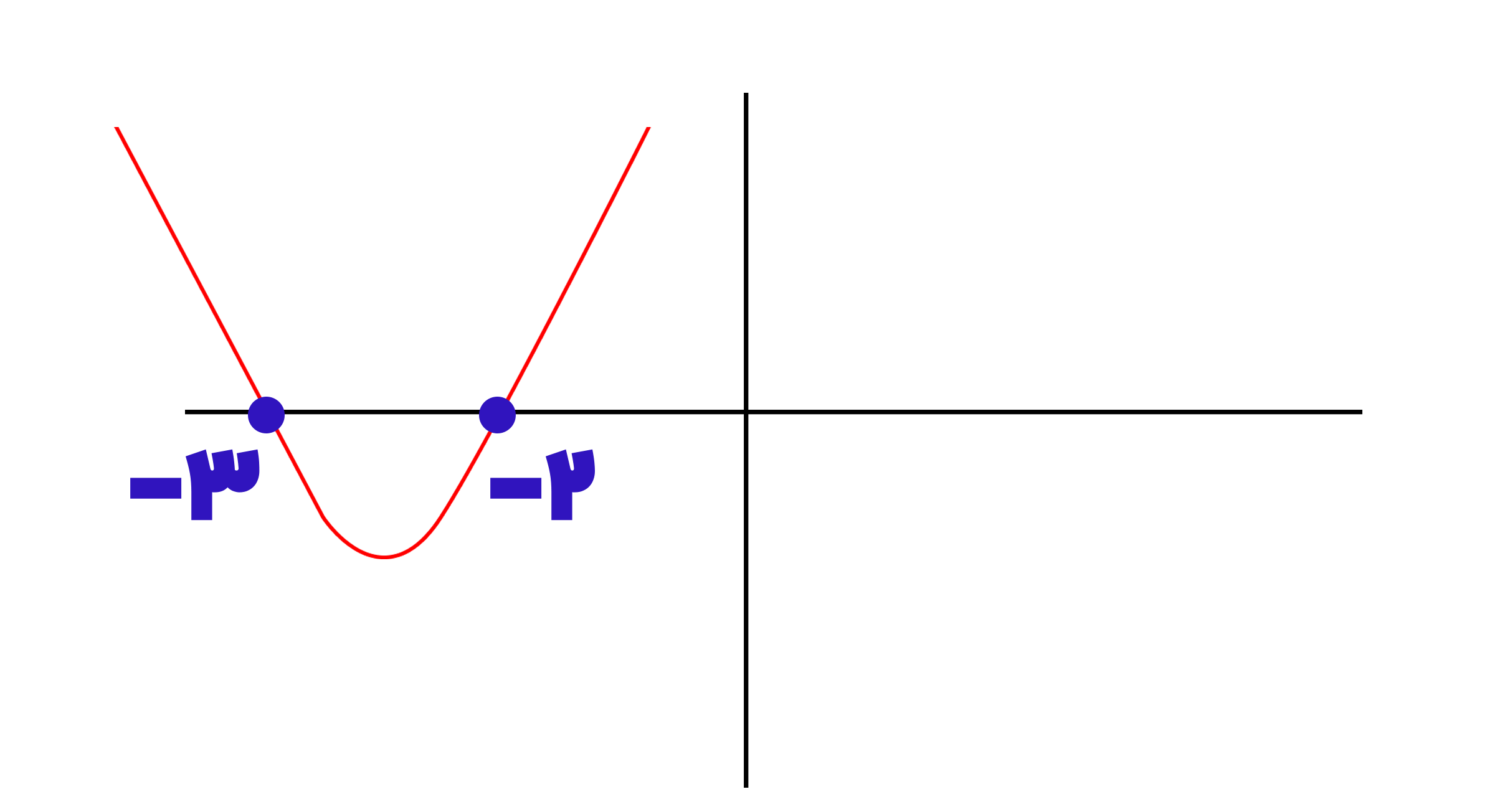
اما یادتان باشد که برای تابع ما شرط تعیین شده بود و نقاط بالای محور x ها و روی محور x ها (ریشه ها) باید در نظر گرفته شوند و هر آنچه که زیر محور x ها باشد جزء شرط داده شده نخواهد بود، بنابراین باید نقاط زیر محور x ها را حذف کرد:

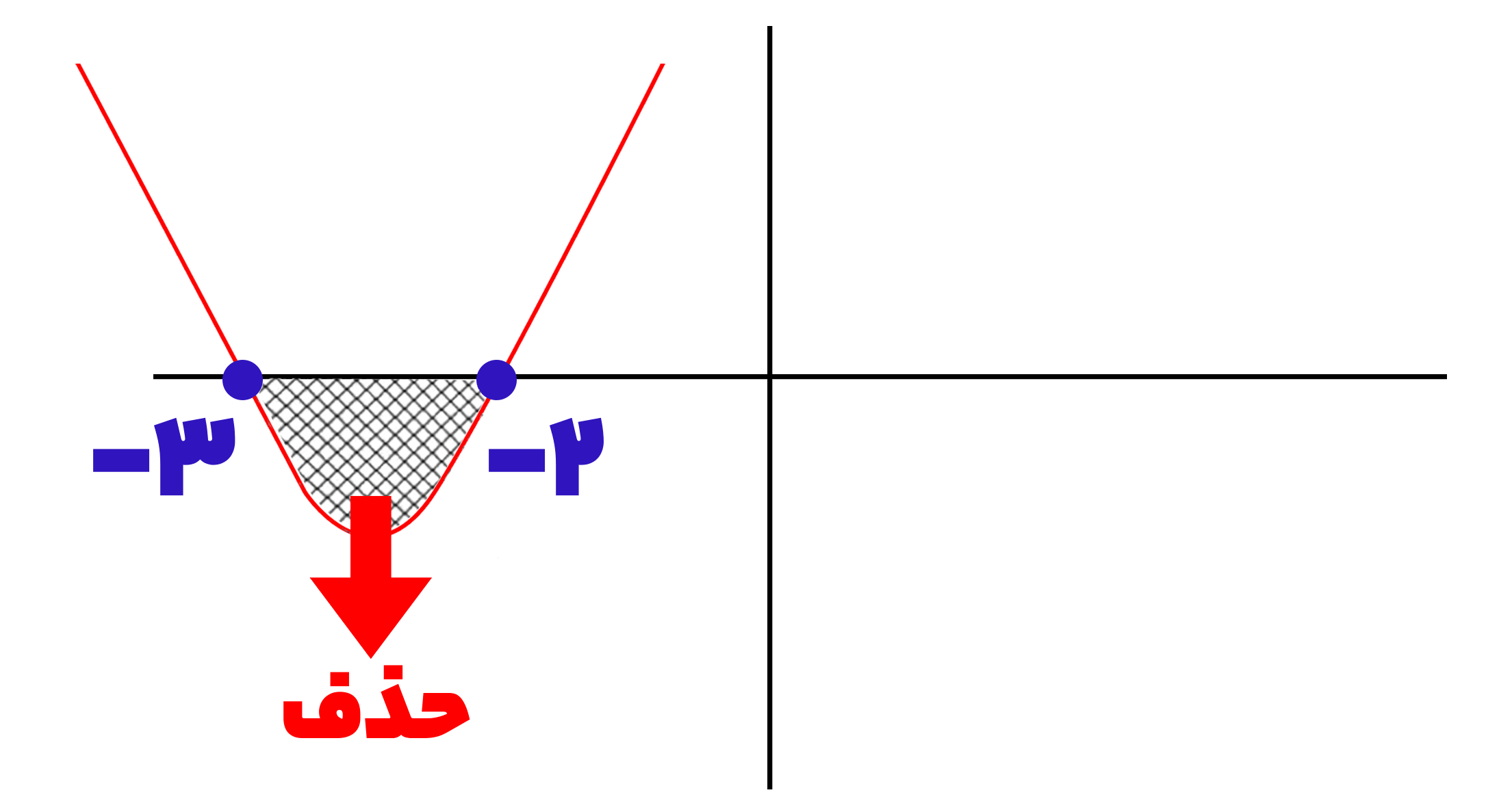
در نتیجه نمودار نهایی ما به شکل زیر خواهد بود:

در نظر داشته باشید برای عبارات کسری که مخرج آنها نیز دارای ریشه هستند، در جدول تعیین علامت در ناحیه ریشه مخرج کلمه ی “ت ن” را می نویسیم که به معنای “تعریف نشده” است. همچنین حواستان باشد که اگر به ریشه های فرد رسیدید تغییر علامت خواهید داشت در غیر این صورت تغییر علامتی در کار نخواهد بود.

منظور از ریشه فرد یا زوج این است که باید به متغیر x خود دقت کنید که توان x شما چند است اگر 1، 3 و … بود پس فرد خواهد بود اما اگر توان 2، یا متغیر x شما در قدر مطلق بود و یا در پرانتزی که توانی زوج داشت، زوج در نظر گرفته می شود و به راحتی می توانید جدول تعیین علامت خود را تکمیل کنید و از نکته بالا استفاده کنید.

به عنوان نکته پایانی یادتان باشد که اگر تابع شما عبارتی کسری و یا چند جمله ای بود، اگر تابع شما دو ریشه داشت از تکنیک 0 > ∆ استفاده نکنید و باید از خارج ریشه های بدست آمده، عددی کمکی را در نظر بگیرید مثلاً عددی بزرگ تر از ریشه دوم در نظر بگیریم و پس از جایگذاری در تابع بررسی کنیم که تابع مثبت، منفی و یا صفر می شود و سپس علامت تابع را مشخص کنیم.

شاید مفید باشد: آموزش تالس