آموزش تابع نمایی در ریاضی
تابع نمایی به تابعی میگویند که متغیر آن در توان باشد، تابع نمایی گفته می شود و به شکل زیر نمایش داده می شود:
y=a^x
در نظر داشته باشید که در این رابطه a همیشه مثبت و مخالف صفر خواهد بود. همچنین دامنه تابع نمایی نیز شامل اعداد حقیقی می باشد و برد آن را اعداد صحیح مثبت تشکیل می دهند. مثل:

رسم نمودار تابع نمایی
به عنوان مثال به تابع زیر نگاه کنید:
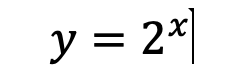
اکنون در نظر داریم با استفاده از آموزش تابع نمایی، شکل تقریبی نمودار را رسم کنیم. بنابراین با توجه به روش نقطه یابی نمودار را ترسیم خواهیم کرد:
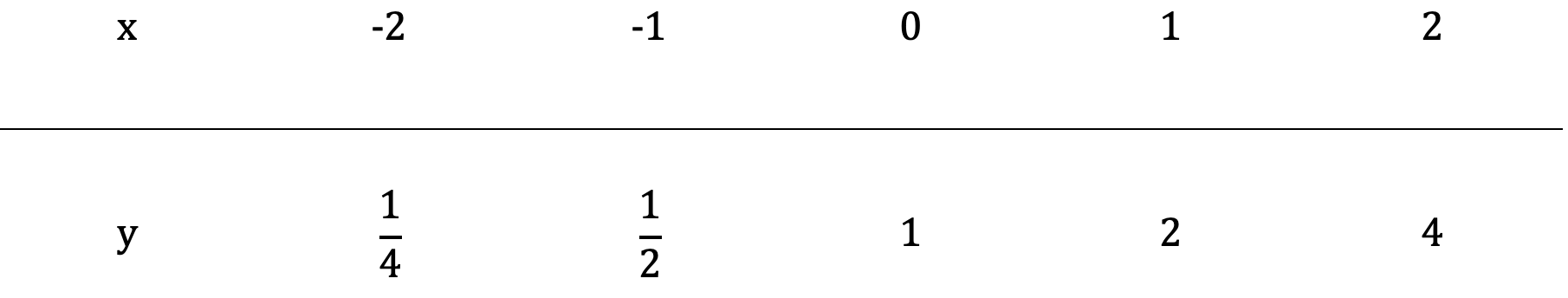
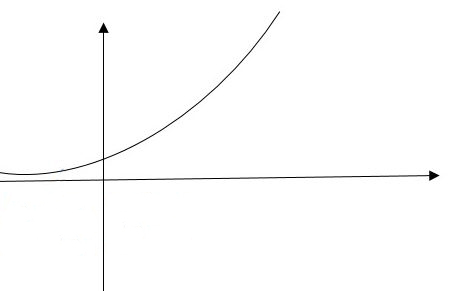
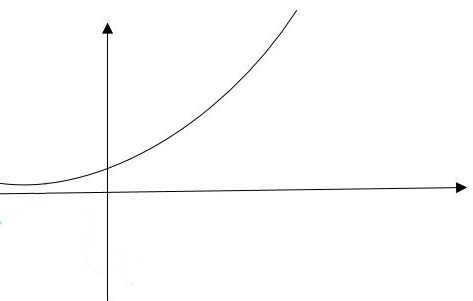
نکته: هرگاه a بزرگتر از یک باشد، نمودار صعودی خواهد بود:
a > 1

همان طور که مشاهده می کند محور y ها را در یک نقطه قطع می کند اما محور x ها را به هیچ عنوان قطع نمی کند.
همان طور که در بالا اشاره کردیم با استفاده روش نقطه یابی شروع به ترسیم نمودار می کنیم:
| 2 | 1 | 0 | -1 | -2 | x |
| 1 | y |
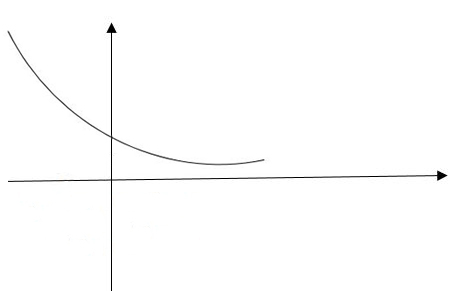
نکته: هرگاه a بین صفر و یک باشد، نمودار نزولی خواهد بود:
(0 < a < 1)

و همان گونه که مشاهده می کنید محور x ها را قطع نکرده اما باز هم در این حالت، محور y ها را در یک نقطه قطع می کند.
بطور کلی نمودار تابع نمایی می تواند به شکل های زیر باشد:
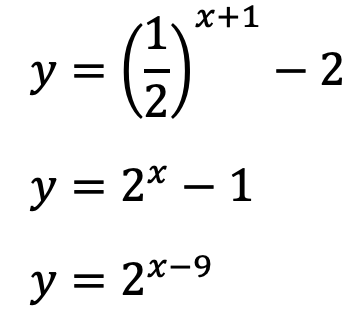
نکته: برای هر مرتبه رسم نمودار تابع نمایی، نیازی نیست که تعداد نقاط بیشماری را در نظر بگیرید. همان گونه که تا به اینجا از آموزش تابع نمایی یاد گرفته ایم، می توانیم با در نظر گرفتن سه نقطه و همچنین با توجه به آشنایی قبلی با نمودار های پایه، اقدام به رسم آنها می کنیم.
در صورتی که در بخش توابع جز صحیح نیز مشکل دارید اینجا کلیک کنید.
جهت استفاده از این روش بایستی مراحل زیر را انجام دهیم:
- اول از همه باید ریشه توانی را پیدا کنیم.
- عدد بدست آمده را جایگزین x می کنیم و y آن نقطه را مشخص می کنیم.
- در آخر x و y بدست آمده را در وسط جدول می نویسیم و یک نقطه قبل و بعد x را جایگذاری می کنیم و y آن نقاط را نیز پیدا می کنیم.به عنوان مثال تابع نمایی y=2^(x-1) را در نظر بگیرید. ریشه توان x = 1 می باشد که به ازای x = 1، مقدار y نیز برابر با یک می شود.
| 2 | 1 | 0 | x |
| 2 | y |
همان گونه که در نمودار مشخص است، هر چقدر x ها به سمت منفی بی نهایت بروند، مقدار y به صفر نزدیک و نزدیک تر می شود اما هیچ گاه به صفر نمی رسد. بنابراین نتیجه می گیریم محور x ها را قطع نخواهد کرد و در کنار آن به سمت بی نهایت حرکت می کند. هنگامی که با مفهوم حد آشنا شوید متوجه می شوید که به این خط، خط مجانب گفته می شود و نمودار آن نیز به سمت بی نهایت خواهد رفت.
بررسی دقیق تر تابع نمایی
سؤالی که وجود دارد این است که آیا همیشه این خط، مجانب محور x ها خواهد بود؟ یادتان باشد که نمودار را می توان از طریق انتقال نیز رسم نمود. اما چگونه؟
تابع نمایی y=2^x را در نظر بگیرید. ابتدا نمودار آن را رسم می کنیم:
| 1 | 0 | -1 | x |
| 2 | y |
همانطور که مشخص است x = 0 ریشه توانی است. طبق جدول بالا یکی از نقاط x منفی شده است. در نتیجه هنگام ترسیم نمودار آن را یک واحد به سمت راست حرکت می دهیم: y^x. در واقع به x ها یک واحد اضافه خواهد شد اما y ها بدون تغییر خواهند ماند:
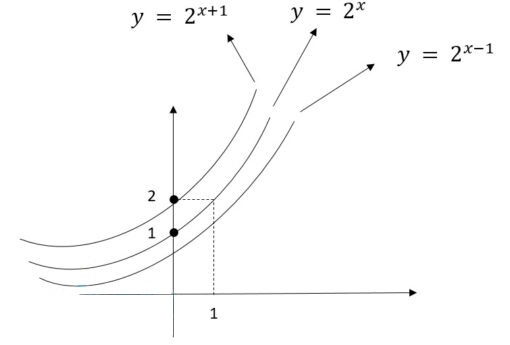
یادتان باشد که همیشه راه نقطه یابی راحت تر و بهترین راه است. اکنون اگر بخواهیم نمودار تابع نمایی y=2^(x+1) را به شیوه انتقال، رسم کنیم. بایستی نمودار را یک واحد به سمت راست انتقال دهیم. در نتیجه نمودار y=2^x بدست خواهد آمد. که نمودار آن در بالا ترسیم شده است.
اما اگر تابع نمایی ما به صورت y=2^x+1 باشد، با توجه به شیوه انتقال، نمدار یک واحد به سمت بالا حرکت می کند. بنابراین در حالت های این چنینی، خط ترسیمی، مجانب محور x ها نخواهد بود و خط y = 1 می شود. به این دلیل که هر مقدار که به x بدهیم، هنگامی که به توان 2 برسید و با یک عدد جمع شود، همیشه مقدار آن تابع از یک بیشتر خواهد شد:
| 1 | 0 | -1 | x |
| 3 | y |
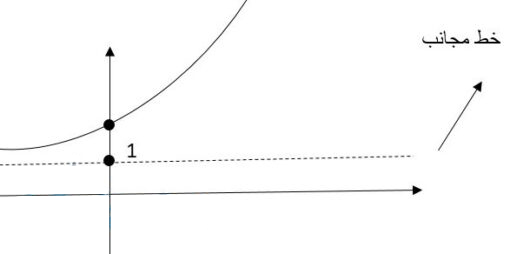
بنابراین باید در رسم نمودار دقت به خرج دهید و به هیچ عنوان اجازه ندهید که نمودار از خط y = 1 پایین تر بیاید.
قرینه تابع نمایی
به تابع زیر دقت کنید:

پس نمودار دو تابع نیز بر اساس آنچه که گفته شد، نسبت به محور y ها قرینه یکدیگر می باشند:
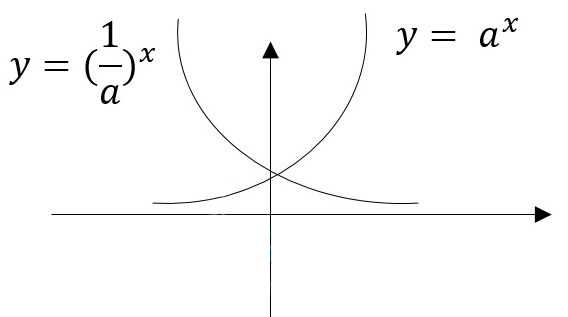
اکنون به دو تابع زیر توجه کنید، به طوری که این دو تابع نسبت به محور x ها نسبت به یکدیگر قرینه هستند:![]()
بنابراین نتیجه می گیریم، اگر x قرینه شود، نمودار نیز نسبت به محور y ها قرینه خواهد شد. اما اگر قرینه شود، نمودار نسبت به محور x ها قرینه خواهد بود.
نکته: در مورد مقایسه دو عدد توان دار با پایه های برابر اگر پایه عدد بزرگتر از یک باشد، هرچه توان بیشتر باشد عدد بزرگتر است. چون در اصل نمودار توابع نمایی با پایه بزرگتر از یک، یک تابع صعودی است. یعنی هر چه x ها بیشتر می شوند yها نیز بزرگتر می شوند.
اما یادتان باشد، زمانی که پایه، عددی بین صفر و یک باشد، نمودار، نزولی می شود. در واقع هر چه توان یا همان x بیشتر شود، y نیز کوچکتر خواهد شد. بنابراین:
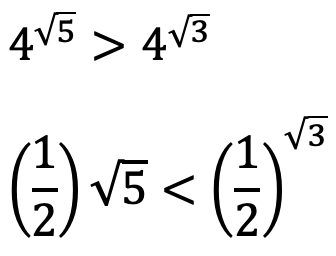
نکته: توابع نمایی، توابع یک به یک هستند. یعنی اینکه به ازای هر x، یک y و همچنین به ازای هر y، یک x، بدست خواهد آمد.
همچنین ببینید: هندسه یازدهم فصل اول











دیدگاهتان را بنویسید