آموزش قضیه تالس

با شما هستیم در آموزش قضیه تالس – در این بخش می خواهیم به درس دوم از فصل دوم کتاب هندسه دهم بپردازیم، یعنی قضیه تالس و کاربرد های قضیه تالس و می خواهیم قضیه تالس را معرفی کنیم، اثبات کنیم و چند نتیجه از آن بگیریم که بسیار نتایج مهم و کاربردی هستند و سپس قضیه تالس را تعمیم می دهیم و به یک نتیجه گیری مهم می رسیم. در پایان نیز عکس قضیه تالس را بیان می کنیم و همچنین اثباتی برای آن ارائه خواهیم کرد.

دانلود جزوه الس

فرض کنید یک مثلث به نام ABC داریم:

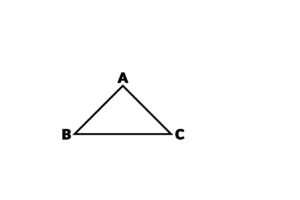
و نقطه D روی ضلع AB قرار دارد:

از نقطه D به موازات ضلع BC رسم می کنیم، به طوری که ضلع AC را در نقطه E قطع کند:

الان متوجه می شویم که DE موازی با BC است:

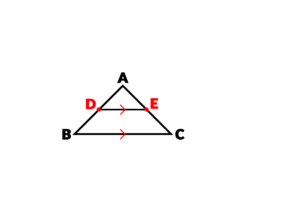
همان طور که مشاهده می کنید روی شکل 4 پاره خط ایجاد شده است:

1. AD
2. BD
3. AE
4. EC

حالا می خواهیم ببینیم این 4 پاره خط با یکدیگر رابطه طولی دارند و اینکه نسبتی بین آنها برقرار هست یا که خیر. برای این کار نقاط را بصورت ضربدری به یکدیگر متصل می کنیم:

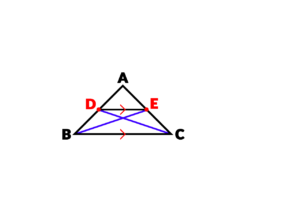
مثلث ADC را در نظر بگیرید:

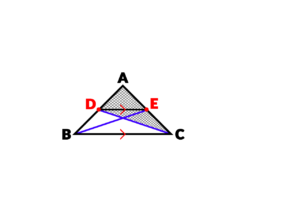
اگر به قسمت هاشور خورده دقت کنید، دو مثلث جای گرفته است؛ یکی مثلث DAE و دیگری مثلث DEC:

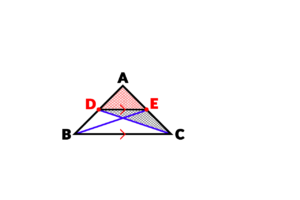
اگر به خوبی توجه کنید هر دو مثلث در رأس D مشترک هستند. یک نکته کلی وجود دارد که اگر دو مثلث در یک رأس مشترک باشند و ضلع های مقابل آنها نیز در یک راستا قرار داشته باشند، دارای ارتفاع های برابر می شوند:

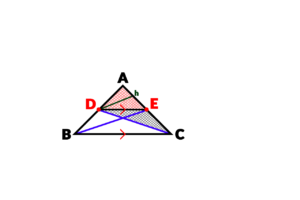
به عنوان مثال ارتفاع h بین هر دو مثلث مشترک می باشد. در نتیجه نسبت مساحت های آنها که همان حاصلضرب ارتفاع در قاعده است، به این دلیل که ارتفاع ها در هر دو مثلث مشترک است از طرفین خط می خورد و نسبت مساحت های آنها نسبت قاعده های دو مثلث خواهد شد:

مشابه همین اتفاق را نیز برای مثلث AEB خواهیم دشت. یعنی در مثلث AEB نیز دو مثلث وجود دارد که در رأس E مشترک هستند؛ یکی مثلث EAD و دیگری مثلث EDB، مجدداً در رأس E مشترک و ضلع های مقابل در یک راستا قرار دارند، در نتیجه ارتفاع های برابری خواهند داشت:

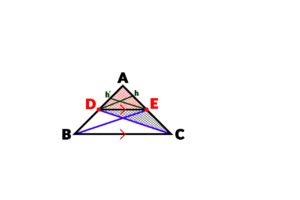
بنابراین مجدداً نسبت مساحت های آنها نسبت قاعده هایشان خواهد بود:

به دو تساوی نوشته کاملاً دقت کنید، DAE و EAD در واقع یک مثلث هستند و صورت هر دو تساوی یکسان است، مثلث DEC و EDB نیز اگر دقت کنید مساحت های مساوی با هم دارند. به این علت که این دو مثلث قاعده مشترک شان DE است و ارتفاع مشترک آنها نیز h می باشد:

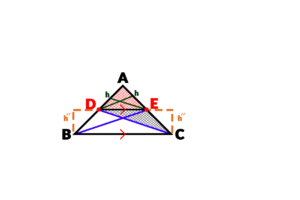
این ارتفاع بین هر دو مشترک است. پس به علت اینکه ارتفاع برابری دارند و همچنین قاعده یکسانی نیز دارند، در نتیجه مساحت آنها نیز با یکدیگر برابر است:

S DBE=S DEC

با توجه به این موضوع نتیجه می گیریم که سمت چپ این تساوی ها با یکدیگر برابر هستند، در نتیجه سمت راست تساوی ها نیز باید با یکدیگر برابر باشند:

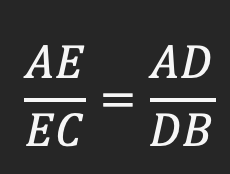
اگر به تناسب بالا دقت کنید، 4 پارامتری که بدست آمد دقیقاً همان 4 پاره خطی بودند که به دنبال رابطه آنها با یکدیگر بودیم!

س ما رابطه آن 4 پاره خط را پیدا کردیم. فهمیدیم وقتی در یک مثلث، یک پاره خط موازی با یکی از اضلاع رسم می شود، آن 4 پاره خط با یکدیگر دقیقاً متناسب هستند. به این رابطه بدست آمده قضیه تالس می گویند:

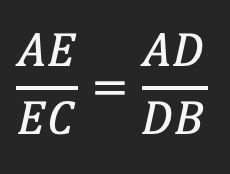
اکنون می خواهیم نتیجه آموزش قضیه تالس را بررسی کنیم و تناسب بدست آمده قضیه تالس را ترکیب در مخرج کنیم. یعنی اینکه صورت را با مخرج جمع کنیم و در مخرج قرار دهیم. به بیان ساده تر، صورت را دست نزنیم ولی مخرج کسر به حاصل جمع صورت و مخرج تبدیل شود و این کار را برای هر دو طرف تساوی انجام دهیم:

یادتان باشد که این موضوع در کاب با عنوان “استفاده ز قضایای تناسب” گفته می شود و اگر با این عنوان مواجه شدید به این منظور است که باید ترکیب در مخرج انجام گیرد.

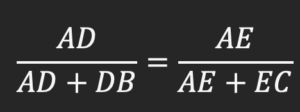
اول از همه نگاه می کنیم ببینیم AD + DB چه می شود؛ این حاصل جمع معادل کل ضلع AB خواهد بود بنابراین می توانیم به جای این عبارت AB بنویسیم. در سمت راست تساوی نیز بجای AE + EC می توانیم کل ضلع AC را بنویسیم:

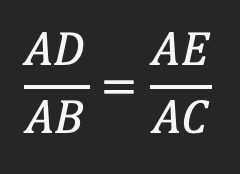
این رابطه بدست آمده بسیار رابطه مهمی است که به آن “رابطه جزء به کل” می گوئیم. صورت اصلی قضیه تالس جزء به جزء می باشد یعنی AD به DB و AE به EC می باشد اما نتیجه به دست آمده جزء به کل است یعنی AD به کل AB، AE به کل EC.

اکنون می خواهیم از نتیجه ای که بدست آورده ایم نتیجه دیگری نیز بگیریم. این مرتبه تفضیل در صورت انجام می دهیم. در واقع AB را از AD کم می کنیم و در صورت تساوی قرار دهیم. اگر کل AB را از AD کم کنیم، پاره خط BD باقی می ماند. برای سمت راست تساوی نیز دقیقاًهمین کار را انجام می دهیم:

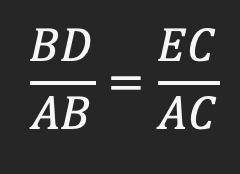
این رابطه بدست آمده باز هم یک رابطه جزء به کل می باشد اما از پایین به بالا. بنابراین نتیجه می گیریم که قضیه تالس را می توانیم هم از بالا و هم از پایین بنویسیم.

نتیجه های 1 و 2، نتایج قضیه تالس هستند که در جای خود کارایی خواهند داشت اما رابطه اصلی که شما باید با آن سر و کار داشته باشید رابطه جزء به جزء می باشد.

تعمیم قضیه تالس

یک بحث تکمیلی در قضیه تالس داریم که آن هم تعمیم قضیه تالس می باشد. رابطه های جزء به کلی که به عنوان نتایج قضیه تالس به آن رسیدیم، می خواهیم رابطه های بدست آمده را تعمیم دهیم و نشان دهیم که تناسب بدست آمده برابر با موارد دیگری نیز هست. آن مورد دیگر پاره خط DE و BC است.

برای پیدا کردن آن رابطه از نقطه E به موازات ضلع AB خطی را رسم می کنیم:

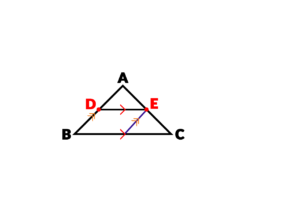
فرض کنیم نقطه ای که پاره خط BC را قع کرده است F باشد:

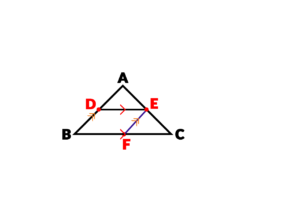
اتفاقی که رخ می دهد این است که چون 2 پاره خط داریم، می توانیم 2 قضیه تالس بنویسیم، قضیه اول مربوط به دو پاره خط موازی DE و BC است: (باید جزء به کل بالا به پایین را بنویسید)

قضیه تالس بعدی را می خواهیم از پایین به بالا بنویسیم، یعنی شما از نقطه C به مقابل نگاه کنید، چیزی که مشاهده می شود یک پاره خط EF دیده می شود که موازی با پاره خط AB است:

برای اینکه سمت راست دو تساوی با یکدیگر یکسان شود قضیه اول را نیز جز به کل می نویسیم. اگر دقت داشته باشید نسبت AE به AC همان جزء به کل از بالا در رابطه اصلی است، در نتیجه:

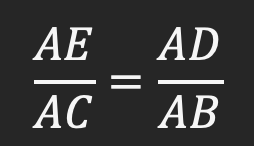
این دو رابطه بدست آمده دقیقا یک طرف تساوی های شان یکسان است، در نتیجه طرف دوم آنها نیز باید با یکدیگر مساوی باشد:

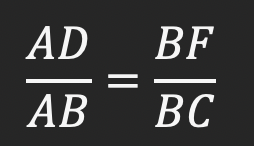
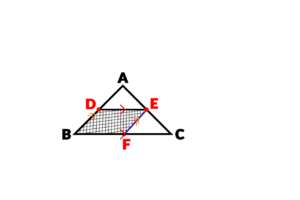
چهار ضلعی بوجود آمده را مشاهده کنید، این چهار ضلعی اضلاع مقابل آن دو به دو موازی هستند و ما به این چهار ضلعی با این خصوصیت “متوازی الاضلاع” می گوییم. یکی دیگر از ویژگی های متوازی الاضلاع این است که اضلاع مقابل با یکدیگر مساوی هم هستند. پس در نتیجه به جای BF می توانیم DE را جایگذاری کنیم.

پس نتیجه می گیریم بخاطر اینکه چهار ضلعی DEBF متوازی الاضلاع است، BF را با DE می توانیم جایگزین کنیم:

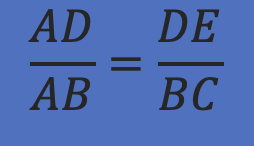
این نتیجه ای است که می خواستیم به آن برسیم. سمت چپ تساوی جزء به کل از بالا است برابر شد با DE به BC. پس در رابطه اصلی تناسب را ادامه (تعمیم) می دهیم:

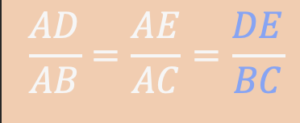
پس نتیجه می گیریم پاره خط های موازی

ریاضی یازدهم فصل دوم تالس

اگر خاطرتان اشد بای نوشتن عکس یک قضیه باید جای فرض و حکم آن را عوض کنیم. ابتدا قضیه تالس را می نویسیم و سپس فرض و حکم آن را مشخص می کنیم.

قضیه تالس:

اگر خطی به موازات یکی از اضلاع مثلث رسم شود و دو ضلع دیگر را قطع کند، آنگاه چهار پاره خط ایجاد شده با یکدیگر متناسب اند.

همان طور که اشاره کردیم برای نوشتن عکس این قضیه باید جای فرض و حکم آن را عوض کنیم:

عکس قضیه تالس هندسه دهم

ببینید: آموزش هندسه 1

اگر چهار پاره خط ایجاد شده توسط خطی که روی دو ضلع مثلث بنا شده، با یکدیگر متناسب باشند، آنگاه آن خط با ضلع سوم مثلث، موازی است.

اکنون باید این تعاریف را به صورت ریاضی بیان کنیم:

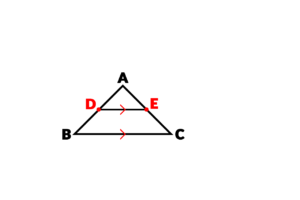
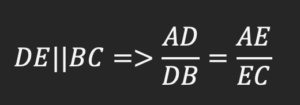
در عکس قضیه جای فرض و حکم را تغییر می دهیم:

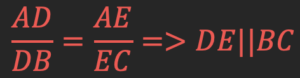
پس نتیجه ای که از عکس قضیه تالس بدست می آید موازی بودن دو پاره خط است. ما در بسیاری از مسائل هندسه احتیاج داریم که بدانیم آیا دو خط با یکدیگر موازی هستند یا خیر؛ در نتیجه یکی از راه های آن این است که بررسی کنیم که آیا قضیه تالس در آن برقرار است یا خیر.

اثبات عکس قضیه تالس

فرض ما این است که پاره خط ها با یکدیگر متناسب هستند و اکنون می خواهیم ثابت کنیم MN موازی BC است:

اگر از فصل اول به خاطر داشته باشید، یکی از مهم ترین کاربرد های برهان خلف، در اثبات عکس قضایا است. در اینجا نیز می خواهیم عکس قضیه تالس را با برهان خلف ثابت کنیم.

برهان خلف می گفت در مرحله اول بزن زیر حُکمت!

هر چه که هست را بگویید نیست و هر چه نیست را بگویید هست، اینجا می گوید MN موازی BC است ما می گوییم نیست:

اگر MN با BC موازی نباشد بالاخره از یک نقطه خارج یک خط باید یک خط موازی بتوان رسم کرد:

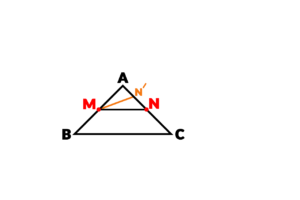
پس فرض می گیریم که MN’ موازی با BC است:

ریاضی یازدهم فصل دوم تالس

اگر دو پاره خط در یک مثلث با یکدیگر موازی باشند قضیه تالس برقرار خواهد بود، و همان طور که قبلاً اشاره کردیم در اثبات عکس قضایا می توان به طور قطع از خود قضایا استفاده کرد، به این دلیل که خود قضیه را قبلاً اثبات کرده ایم، پس با توجه به خود قضیه تالس:

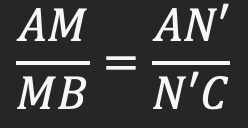
در اینجا یک فرض هم داشتیم، فرض را هم در کنار رابطه تالس می نویسیم:

با توجه به اینکه سمت چپ تساوی با یکدیگر برابر هستند در نتیجه سمت راست تساوی نیز باید برابر باشند:

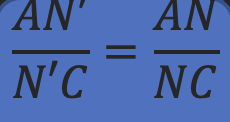
این اتفاق فقط زمانی رخ می دهد که N’ دقیقا همان N باشد، پس در اینجا با یک تناقض روبرو شدیم، به این دلیل که می دانیم N’ با N برابر نیست و دو نقطه متفاوت از هم هستند.

به این دلیل که با یک اصل بدیهی به تناقض خوردیم، نتیجه می گیریم که حکم اولیه که زیر آن زدیم خودش درست بود. یعنی MN موازی با BC است.

یادتان باشد تنها رابطه ای که در آن طول پاره خط موازی را داشت، همان تعمیم قضیه تالس است