آموزش دایره مثلثاتی

آموزش دایره مثلثاتی، به دایره‌ ی با شعاع واحد گفته می‌شود و با استفاده از این دایره‌ به  سادگی می‌توان نسبت‌های مثلثاتی (سینوس، کسینوس و تانژانت) را بدست آوریم. همچنین با استفاده از مفهوم دایره‌ی مثلثاتی، طول‌ها و زوایا را در اشکال هندسی مختلف می توان بدست آورد.

فیلم آموزشی دایره مثلثاتی

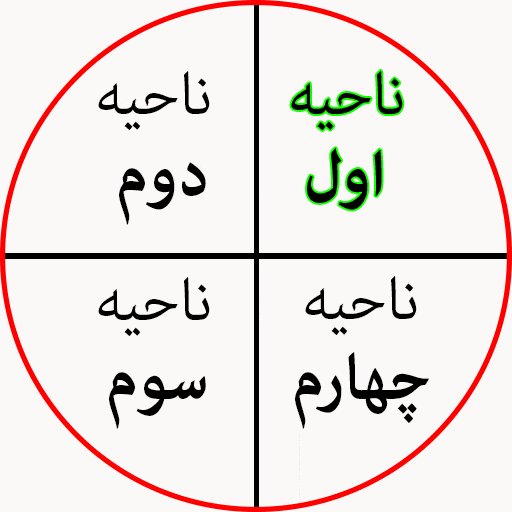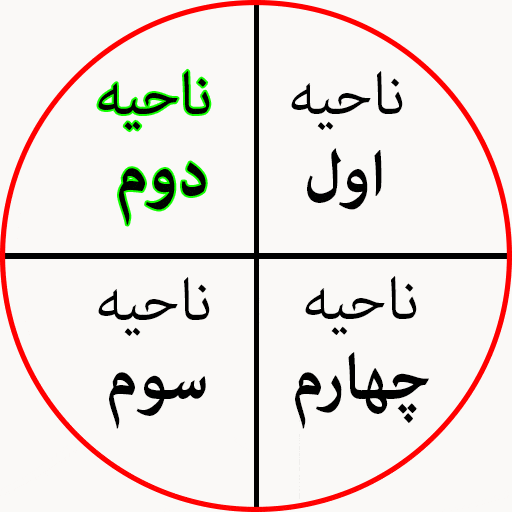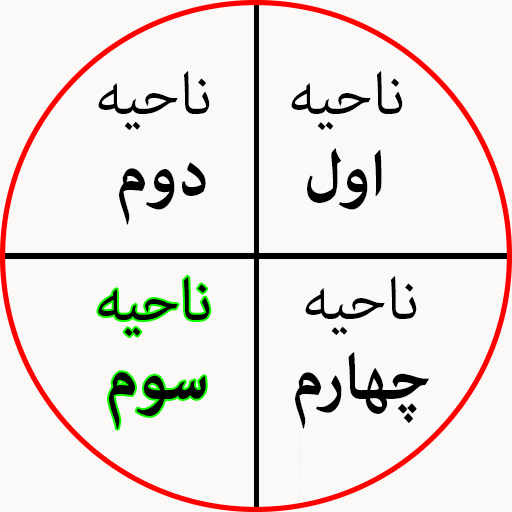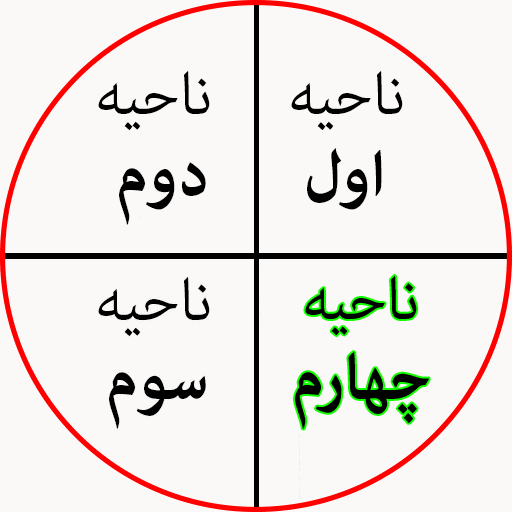
ربع های دایره مثلثاتی

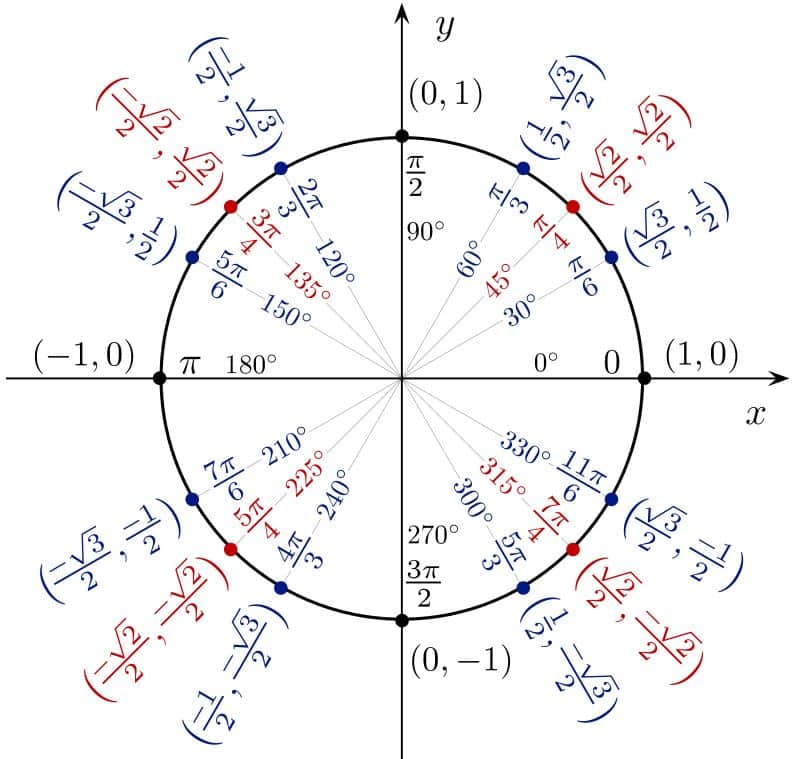
حتماً از ریاضیات پایه تحصیلی هفتم و هشتم به یاد دارید که طبق قرارداد بین المللی، دایره به 360 درجه تقسیم می شود. بنابراین اگر دایره را به 4 قسمت مساوی تقسیم کنیم هر کدام از این قسمت ها 90 درجه خواهند شد. بنا بر تعریف، اگر در خلاف جهت عقربه های ساعت حرکت داشته باشیم، زاویه مثبت ایجاد می شود در نتیجه زاویه هایی که روی چهار رأس دایره به وجود می آیند به ترتیب مقدار های 0، 90، 180، 270 و 360 درجه خواهند بود. برای درک بهتر این موضوع به دایره مثلثاتی زیر دقت کنید.

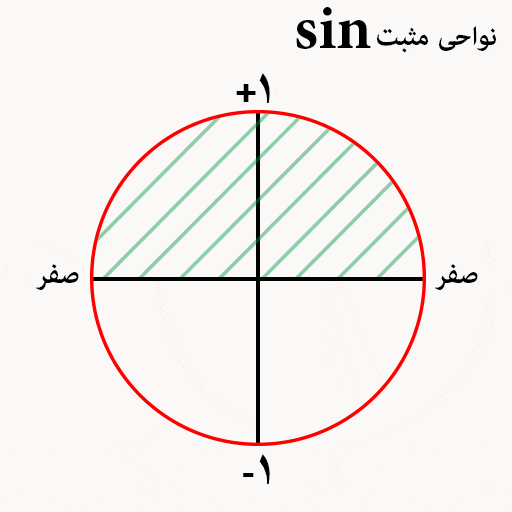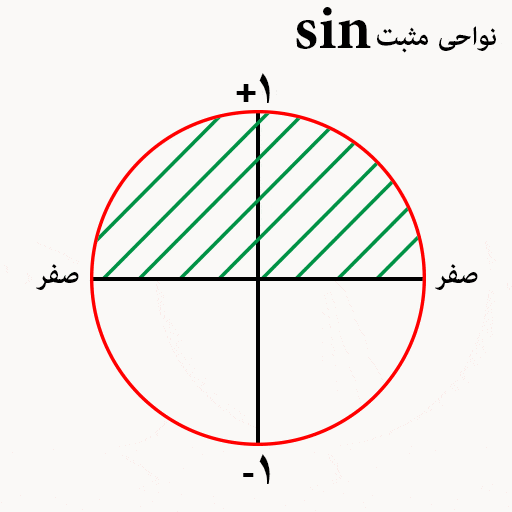
سینوس در دایره مثلثاتی

یکی از نکاتی که درون دایره مثلثاتی به خوبی می‌توان نشان داد ناحیه‌ های مثبت و منفی دایره مثلثاتی است. در ناحیه اول و دوم سینوس مثبت است و در ناحیه سوم و چهارم سینوس منفی است.

همچنین ببینید: آموزش لگاریتم   –   آموزش تعیین علامت

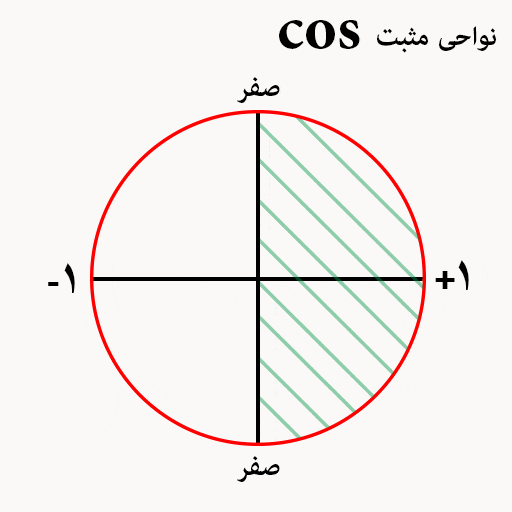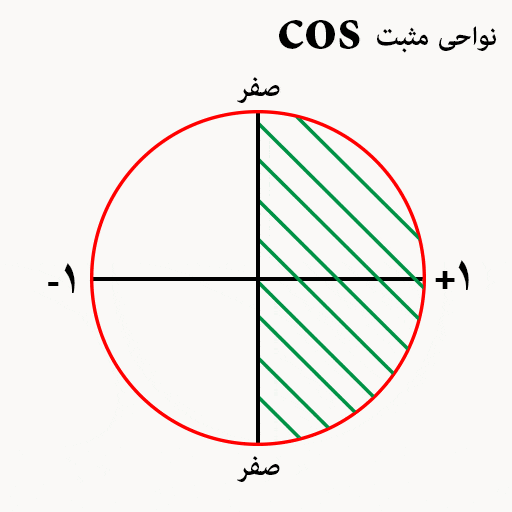
کسینوس در دایر مثلثاتی

مثل دایره مثلثاتی سینوس‌ ها در دایره مثلثاتی کسینوس ‌ها دو ناحیه مثبت و دو ناحیه منفی داریم ، ضمنا بهتر است که مقادیر زوایای صفر ، 90 ، 180 ، 270 و 360 درجه را درون دایره مثلثاتی حفظ کنید.

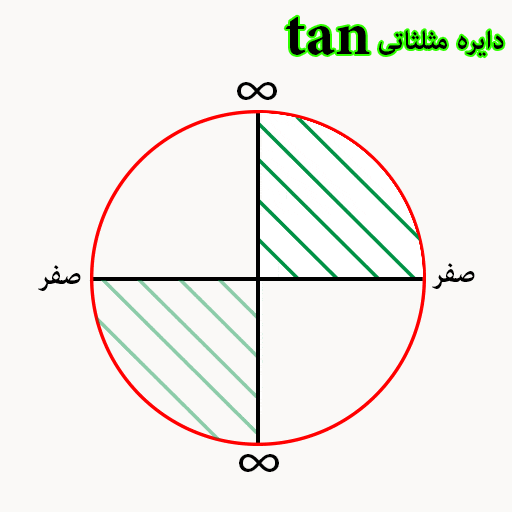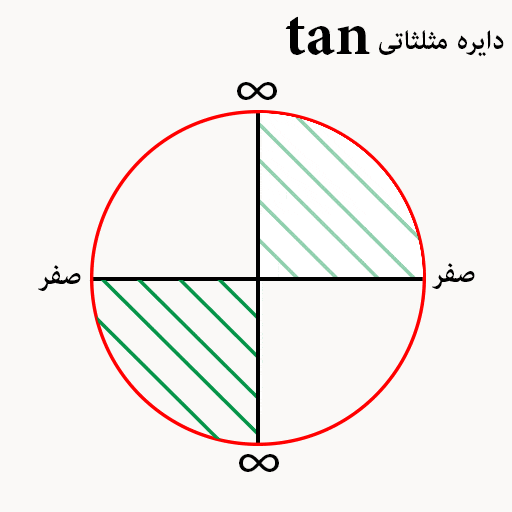
تانژانت در دایره مثلثاتی

در دایره مثلثاتی تانژانت 1+ و 1- وجود ندارد. صفر های تانژانت مثل سینوس هست و به جای مثبت و منفی یک علامت بینهایت باید قرار دهیم. پس مجدداً تاکید می‌ کنیم در دایره تانژانت بجای مثبت و منفی یک علامت بی ‌نهایت گذاشته می‌شود.

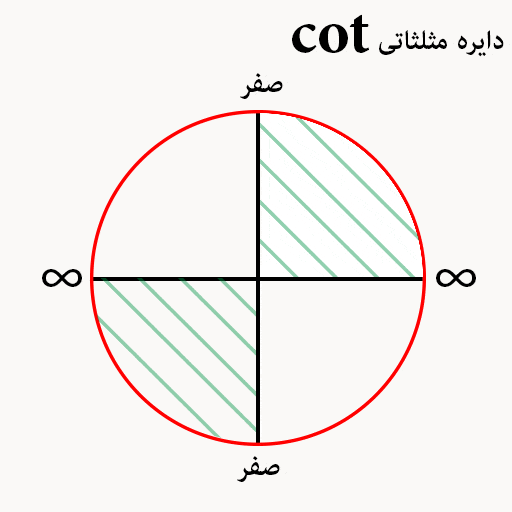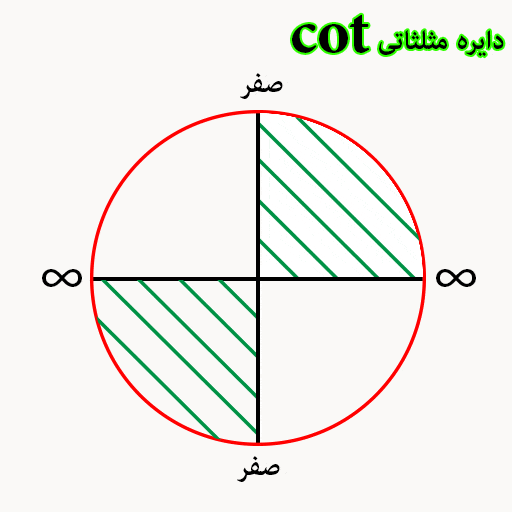
کوتانژانت در دایره

صفر های دایره مثلثاتی cot مثل دایره مثلثاتی Cos است ولی بجای مثبت و منفی یک ، باید علامت بینهایت قرار دهیم.

کاربرد دایره مثلثاتی

محاسبه سینوس، کسینوس و تانژانت

دایره ای به شعاع 1 واحد را رسیم می کنیم:

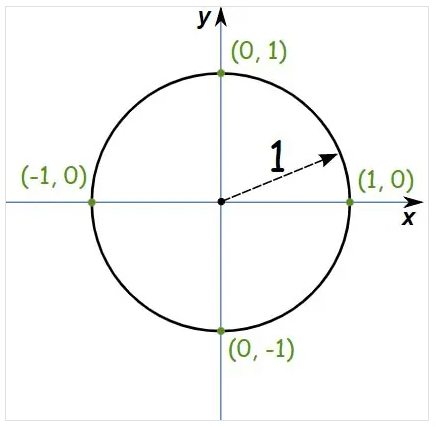
همان طور که مشاده می کنید شعاع دایره برابر با 1 می باشد و به همان خاطر می توانیم نسبت های مثلثاتی را بطور مستقیم محاسبه کنیم. بطور مثال قصد داریم نسبت های مثلثاتی را در یک زاویه خاص بدست آوریم. برای این کار دایره را در زاویه مورد نظر قرار می دهیم و از آن به مرکز دایره خطی رسم می کنیم. واضح است که طول این خط برابر 1 واحد خواهد بود. بنابراین ارتفاع نقطه مورد نظر تا محور افق، برابر با سینوس خواهد بود و طول افقی نقطه تا مرکز دایره، مقدار کسینوس زاویه ی مورد نظر را نشان می دهد. اگر در زاویه مورد نظر ما خطی به دایره مماس شود، طول آن تعیین کننده مقدار تانژانت زاویه خواهد بود.

در شکل زیر دایره مثلثاتی، اندازه سینوس، کسینوس و تانژانت زاویه θ نمایش داده شده است:

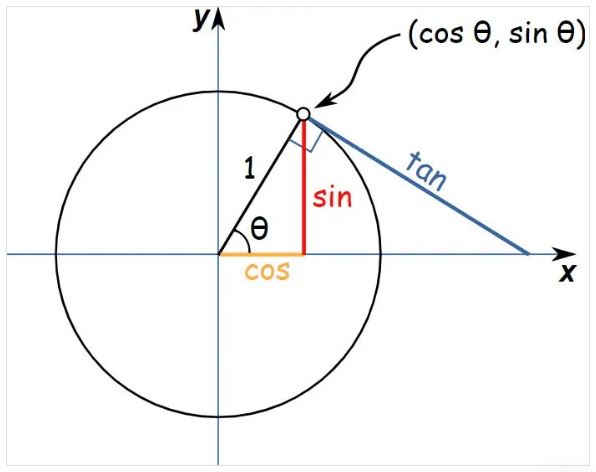
همان طور که ملاحظه می کنید طول خط قرمز رنگ، مشخص کننده سینوس، طول خط زرد رنگ، مشخص کننده کسینوس و خط آبی رنگ معادل اندازه تانژانت می باشد. به عنوان مثال می دانید که سینوس زاویه صفر درجه معادل صفر خواهد بود (sin0=0)، اکنون قصد داریم با استفاده از دایره مثلثاتی، این عدد را بدست آوریم. منظور از زاویه صفر درجه این است که نقطه دقیقاً روی محور افقی (xها) قرار دارد.

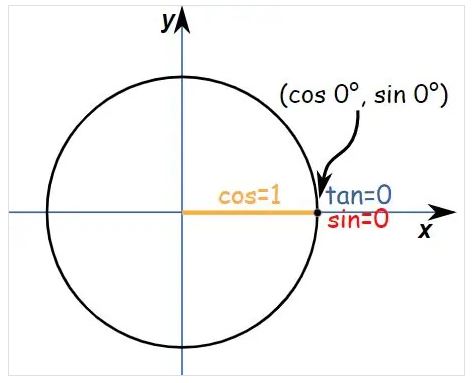
با توجه به محور مختصاتی بالا، فاصله عمودی نقطه تا محور افقی (یا همان میزان ارتفاع نقطه) برابر با صفر خواهد بود. پس نتیجه می گیریم که sin0=0 می باشد. همچنین مشخص است که فاصله نقطه تا محور عمودی برابر با میزان شعاع دایره است که این مقدار مشخص کننده میزان کسینوس است:

sin(0)=0

cos(0)=1

حالا یک نقطه در زاویه 60 درجه نسبت به محور افقی در نظر بگیرید. با در نظر گرفتن طول های بدست آمده می خواهیم مقدار سینوس و کسینوس را در زاویه 60 درجه محاسبه کنیم:

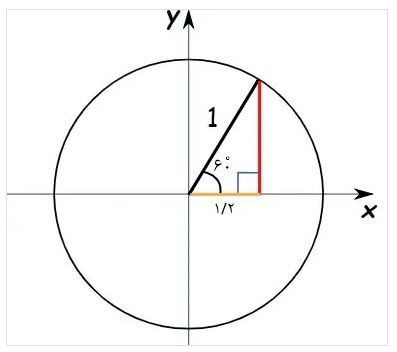
طبق محور مختصاتی ترسیم شده، اندازه طول رد رنگ برابر با یک وم و اندازه طول قرمز رنگ معادل 0.866 خواهد بود (اگر اندازه گیری انجام شود این عدد بدست خواهد آمد) . پس با توجه به محاسبات صورت گرفته می توان نتیجه گرفت:

sin(60)=0.866

در نظر داشته باشید که علامت مقادیر مثلثاتی با استفاده از قوانین کارتزین تعیین می شوند. به عنوان مثال اگر نقطه ای در ربع سوم دایره مثلثاتی باشد هم مقدار سینوس و هم مقدار کسینوس آن نقطه منفی خواهد شد.

فیثاغورس

همان طور که می دانید قانون فیثاغورس عنوان می کند که در یک مثلث قائم الزاویه، حاصل جمع مربع اضلاع برابر با مربع وتر خواهد بود. در نتیجه در دایره مثلثاتی نیز این قضیه برقرار است:

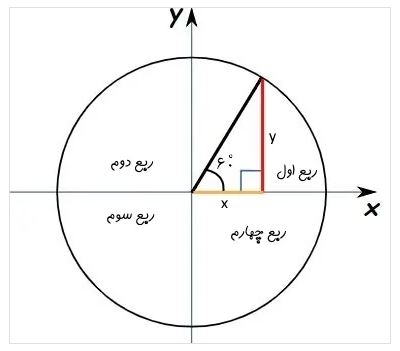
x^2+y^2=1

اگر در رابطه بالا، مقدار های متناظر با x و y را جایگذاری کنیم، خواهیم داشت:

جدول دایره مثلثاتی

در محاسبات مثلثاتی، زاویه های پر کاربری وجود دارند که در بسیاری از مسائل به طور قابل توجهی تکرار می شوند. در جدول زیر این زاویه های به همراه مقدار مثلثاتی شان ارائه شده است:

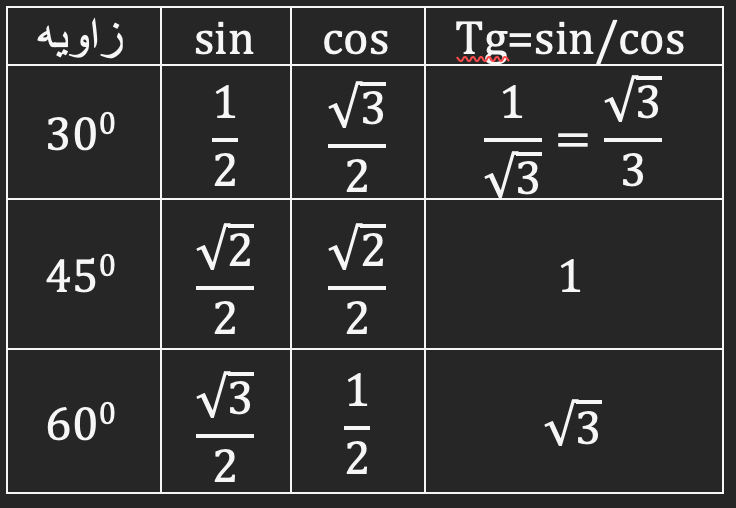
برای اینکه راحت تر مقادیر را به خاطر بسپارید مقدار های جدول بالا را به ترتیب از 1 تا 3 بشمرید و آن ها زیر رادیکال قرار دهید و همه را به 2 تقسیم کنید:

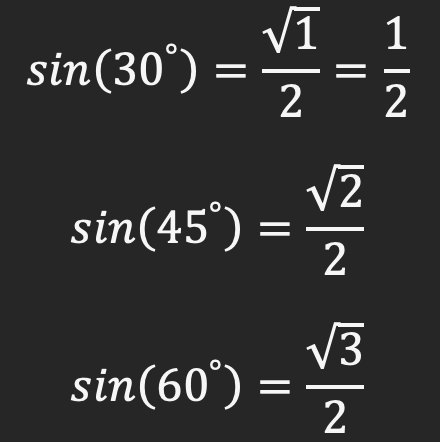
اما برای کسینوس به صورت برعکس عمل کنید و از 3 به 1 شمارش را انجام دهید:

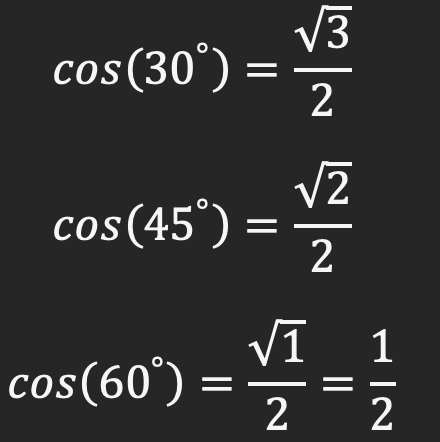
تانژانت د دایره مثلثاتی

با توجه به تعریف های مثلثاتی، اندازه تانژانت برابر است با حاصل قسیم سینوس به کسینوس یک زاویه. به عنوان مثال طبق جدول زوایای مهم که در بالا به آن اشاره شد مقدار کسینوس و سینوس برای زاویه 30 درجه مشخص هستند بنابراین به راحتی می توان مقدار تانژانت را نیز محاسبه کرد:

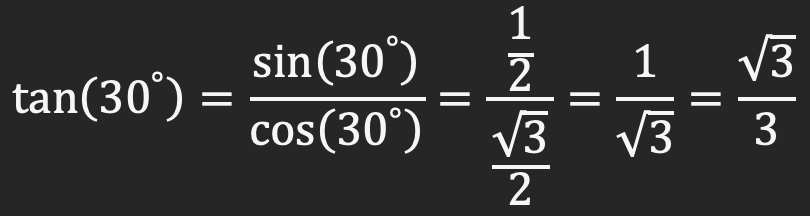
تمامی دایره

علامت مقدار های سینوس و کسینوس بعد از 90 درجه متفاوت هستند و در واقع هر کدام از ربع های دایره مثلثاتی روی علامت سینوس و کسینوس تأثیر می گذارند. با توجه به محور مختصاتی زیر علامت های سینوس در سمت راست و علامت های کسینوس در سمت چپ هر ربع نشان داده شده است:

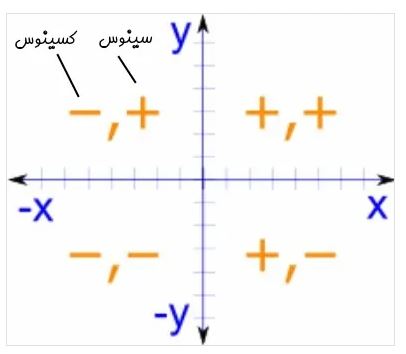
با توجه به محور بالا در سمت راست دایره مثلثاتی مقدار های کسینوس مثبت خواهد بود و همین طور در نیمه بالایی دایره مثلثاتی مقدار های سینوس مثبت هستند. عکس این علامت ها نیز در نیمه دیگر دایره مثلثاتی اتفاق افتاده است. در شکل زیر مقدار های سینوس و کسینوس در زاویه های مختلف توضیح داده شده است. به نحوه تکرار شدن اعداد و تغییر علامت ها به خوبی دقت کنید.