رسم توابع به کمک انتقال – انتقال تابع

رسم توابع به کمک انتقال یا انتقال تابع یکی از موضوعات ریاضی 3 است که بعد از مشاهده این مطلب به صورت کامل آن را یاد میگیرد 😉
يكی از پايه ترين دروس كنكور و البته كه بيشترين سوالات رياضی در رابطه با آن طرح می شود، قطعا مبحث توابع خواهد بود. توابع به قدری مهم بوده كه آن را در دوره متوسطه دوم پايه رياضی تلقی می كنند، اما برای حل كردن سوالات مربوطه به آن بايد چندين نكته بسيار مهم را در راستای حل كردن آن ها پيشه بگيريد كه سبب شده به پاسخ های صحيح سريع تر دست يابيد.
تعريف تابع: تابع مجموعه ایی می باشد كه در آن مولفه های بسيار زيادی وجود خواهد داشت كه يك مولفه اول و مولفه دوم در هر يك آن ها قرار دارد؛ توجه داشته باشيد كه برای تابع بودن اگر دو عدد مولفه اول همسان بودن بايد مولفه دوم آن ها نيز ثابت باشند و در غير اين صورت ديگر تابع محسوب نخواهد شد، اين موضوع را در بسياری از تست ها مطرح خواهند كرد و بهتر است شما از اهميت اين موضوع خبر داشته باشيد.
در صورتی که در بحث دامنه و برد تابع نیز مشکل دارید با ما همراه باشید.
انتقال تابع
انتقال تابع : سوالات بسيار زيادی در رابطه با تابع بودن نمودار مطرح خواهد شد كه با بررسی عواملی كه الان می گوييم می توانيد درك كنيد كه يك نمودار آيا تابع است و يا خير؟ نموداری كه برای شما در آزمون ها و… رسم شده است را مشاهده كنيد و البته كه خطوط فرضی عمودی نيز را در نظر داشته باشيد، اگر آن ها تمامی نقاط را فقط و فقط در يك نقطه قطع كند آن تابع محسوب خواهد شد و اگر در غير اين صورت باشد قطعا تابع نخواهد بود.
بهتر است بدانيد برخی ديگر از نمودار ها نقطه ایی می باشند كه دانش آموزان برای حل و استدلال آن ها بسيار به مشكل می خورند، كافی است كه خط عمودی فرضی را برای آن ها هم فرض كنيد سپس ببينيد كه در يك نقطه قطع خواهد كرد يا خير.
انتقال تابع با نقطه يابی های جديد:
در اين مقاله انواعی از انتقال های تابع را مرور خواهيم كرد و راهكار های آنها را برای شما ارائه خواهيم داد، نقطه يابی يكی از مطمئن ترين روش هایی می باشد برای انتقال تابع، البته كه اگر اصول آن را فرا گرفته باشيد به راحتی می توانيد نقطه يابی را انجام دهيد. شما برای نقطه يابی فقط كافی است كه جدولی را ترسيم كرده و البته آن را به دو بخش x و y تقسيم كنيد حال نوبت شما خواهد بود كه بفرماييد اگر عدد را به جای x قرار دهيم y ما چه عددی را نشان می دهد و يا به اصطلاح چه تغيير می كند.
انواعی از نمودار ها كه بهتر است حالت آنها را بدانيم:
در برخی از آزمون ها ضابطه ایی برای شما به نمايش در خواهند آورد و در گزينه های پاسخ آن سوال نموداری را ترسيم خواهند كرد و به شما می گويند كه نمودار مربوطه به ظابطه را انتخاب كنيد، برای اين گونه از سوالات روش های بسيار زيادی وجود خواهد داشت كه آن ها در موارد زير شرح خواهيم داد:
- سهمی های مينممی: يكی از سهمی ها،از نوع مينيمم می باشد، آن ها هميشه به اصطلاح دست هايشان رو به بالا است.
- سهمی های ماكسيممی: نوعی ديگر از سهمی ها از نوع ماكسيمم هستند، و البته كه نوع ماكسيممی هميشه دست هايشان رو به پايين هستند.
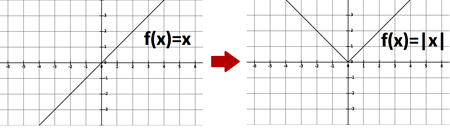
- قدر مطلق: ممكن است كه در برخی از ظابطه ها قدر مطلق برای شما نوشته باشند و كافی است كه شما بدانيد نمودار قدر مطلق ايكس همانند عدد هفت خواهد بود، و البته كه منفی قدر مطلق ايكس هم همانند عدد هشت می باشد، همانند تصوير زير.
- درجه 3، y=x3 : تابع درجه سوم نمودار بسيار آسانی خواهد داشت كه به اصطلاح تابع لر به آن ها گفته می شود به اين دليل كه شبيه به كلمه ( لر ) است،در شكل زير اين موضوع به وضوح مشخص خواهد بود.
- توابع راديكالی: آخرين نوع نمودار های تابع ها از نوع راديكالی هستند، اگر به شما ضابطه ایی به همراه راديكال داده شد بدانيد كه آن نوع از ضابطه ها نموداری ابرو مانند ترسيم خواهند شد كه به اصطلاح به آن ها هم توابعی به شكل ابرو می گويند.
نكته : با توجه به ساختار هر يك از حالاتی كه ممكن است ضابطه به نمايش در بيايد متوجه خواهيد بود كه با هر يك از ضابطه ها چه نموداری نمايش داده خواهد شد.
رسم توابع به کمک انتقال :
تا به الان تمامی نكات مهمی كه شرح داده ايم را اميدوار هستيم كه فرا گرفته باشد و البته در اين بخش به انتقال توابع خواهيم پرداخت مبحثی كه در سه سال دهم و يازدهم و دوازدهم بازتاب بسياری خواهد داشت.
فرض كنيد تابع نمودار تابع f(x) را داشته باشيم و می خواهيم آن را با توجه به نمودار ديگری رسم كنيم، برای اين بخش قطعا بايد به نكات بسيار مهمی حتما توجه كرده باشيد، نظير آنكه هر چه اعمال روی x ها انجام دهيد آن به صورت عكس انجام خواهد داد، اگر شما بنويسد كه x+3 آن به سه واحد منفی خواهد رفت و به عبارتی تمام اعمال ها را به صورت برعكس انجام می دهد كه تاثير بسيار مستقيمی روی y ها هم می گذارد.
برای درك موضوع در بخش بالا به موارد زير به خوبی نگاه كنيد:
- برای رسم كردن نمودار مربوط به f(x+a) كافی است كه ايكس ها را به مقدار a به سمت چپ به اصطلاح هل دهيم.
- برای رسم كردن نمودار f(x- a) فقط و فقط همانند بخش بالا كافی است كه ايكس ها را به مقدار a به سمت راست هل دهيم.
- برای رسم كردن f(x)+b ممكن است با بخش های بالایی كمی تفاوت داشته باشد به اين دليل كه b خارج از پرانتز درون x است، حال شما بايد x ها را به مقدار b به سمت بالا ببريد.
- برای رسم كردن f(x)-b كافی است كه همانند نمودار بالا به مقدار b مانند به پايين آن را سوق دهيم.
- برای به دست آوردن نمودار -f(x)هم كافی است تمام و كل نمودار را نسبت به محور ايكس ها قرينه كنيد.
- رسم كردن نمودار هایی همانندk f(x) كمی ممكن است كه با موارد بالا متفاوت باشد، به آن صورت كه اگر k مثبت باشد قطعا نمودار به اصطلاح جمع خواهد شد و دو طرف نمودار به هم ديگر نزديك خواهد شد و اگر آن منفی باشد به اصطلاح آن بسته خواهد شد.
جمع بندی: انتقال توابع موضوعی است كه طراح كنكور ها در رشته تجربی و رياضی به آن ها بسيار توجه خواهند كرد و البته كه شما با روش های آسانی كه به شما ارائه داديم به راحتی می توانيد سوالات مربوطه با آن ها را حل كنيد، پيشنهاد ما به شما آن است كه شكل و ترسيم نمودار ها را با توجه به ضابطه های آن ها فرا بگيريد كه در تست ها خيلی به شما كمك خواهند كرد.
همچنین ببینید: معکوس ماتریس











دیدگاهتان را بنویسید